こんにちは!さとあずです。
今日は紙が1枚あればできる内容です!
みなさんはこの問題、直感で解けますか?それとも計算して解きますか?
さっそく、いってみましょう〜!
どんな角に近づく?
紙を1枚用意してください。
折り紙のような正方形でもいいし、そこらへんのチラシでも大丈夫です。
紙の端が直線になっていればなんでも構いません。
まず、紙の角をテキトーに折って、折り目①をつけます。(今回は右上端を始めに折ることにします)

その折り目①に上辺が重なるように折り目②をつけます。

折り目②に上辺が重なるように折り目③をつけます。


これを繰り返したときに、2箇所の折り目はそれぞれある直線に近づいていきます。
それぞれどんな直線に近づくでしょうか?
直感で考えてみよう!
左右の折り目が近づく直線をそれぞれ直線①(左側)、直線②(右側)とします。直線①と直線②で分けられた3つの角をそれぞれ角①(左側)、角②(真ん中)、角③(右側)とします。
それぞれ左右の折り目がどのようにして作られた折り目なのかもう一度考えてみましょう。
左側の折り目は、右側の折り目の左側の角を2等分する直線ですよね。言い換えると、角①=角②となるような直線です。
逆に、右側の折り目は、左側の折り目の右側の角を2等分する直線です。言い換えると、角②=角③となるような直線です。
これらを合わせると、角①=角②=角③になるように2つの直線は作られていて、角①+角②+角③=180°なので、どの角も60°になることが予想できます。
よって、2箇所の直線群は180°を三等分する直線に近づくといえます。

ただ、この直感で考える方法は、数学的にいうと、右と真ん中、真ん中と左がそれぞれ大きさが等しくなるだろうというのが、当たり前のようで、証明がなかなか難しかったりします・・・
計算で検証してみよう!
右角を折って、左角を折る一連の操作を1回と数える。
また、3箇所の角を左から角①、角②、角③と呼ぶことにしましょう。
1回目の操作が終わった段階で、右の角(角③)をθ(シータ)とおくと、角①と角②は両方とも、(π-θ)/2となります。(弧度法でπ=180°を表します)
2回目の操作が終わった段階では、左の角(角①)が(π-θ)/2なので、角②と角③はπから角①を引いたものを半分にすればいいので、計算すると、次のようになります。
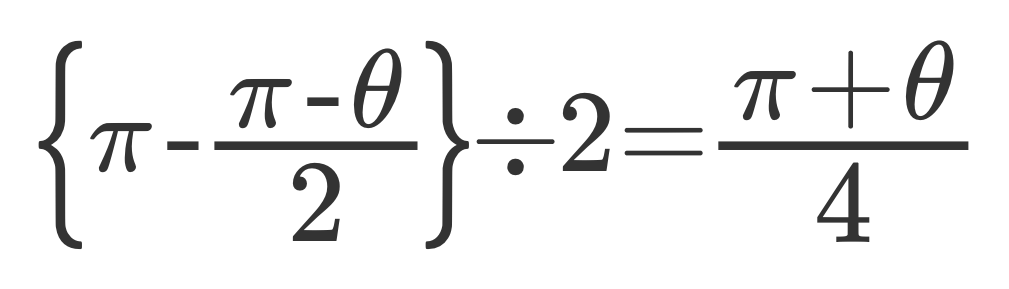
これを続けていくと、次の表のようになります
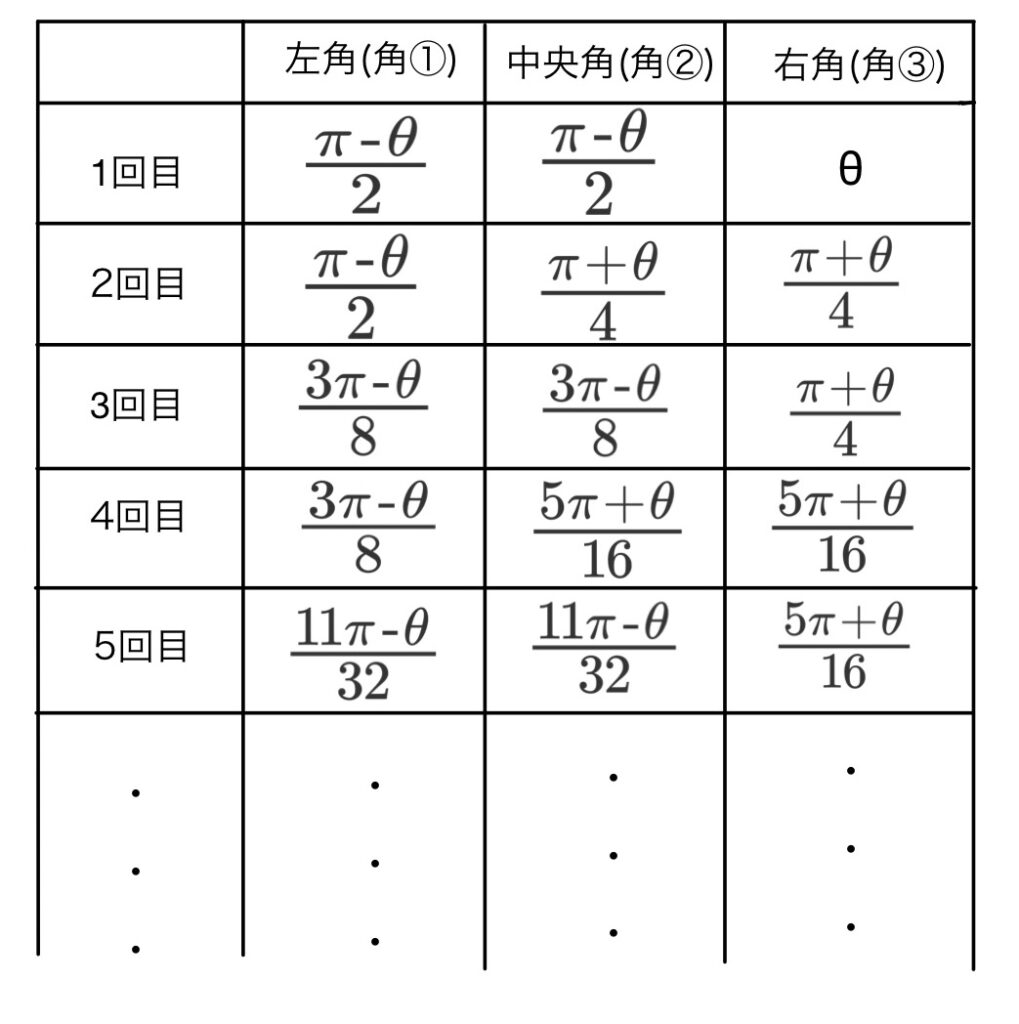
この作業を無限回続けていくと、どのような角に近づいていくのか計算してみよう。
まずは、真ん中の角に注目して考えてみましょう〜
真ん中の角のn回目の操作後の大きさをan考えてみます。
anはπからn-1回目の操作後の角an-1を引いた後、2で割った値なので、
an=(π-an-1)/2
が成り立つ。
よって、次のように漸化式を解けば良い。

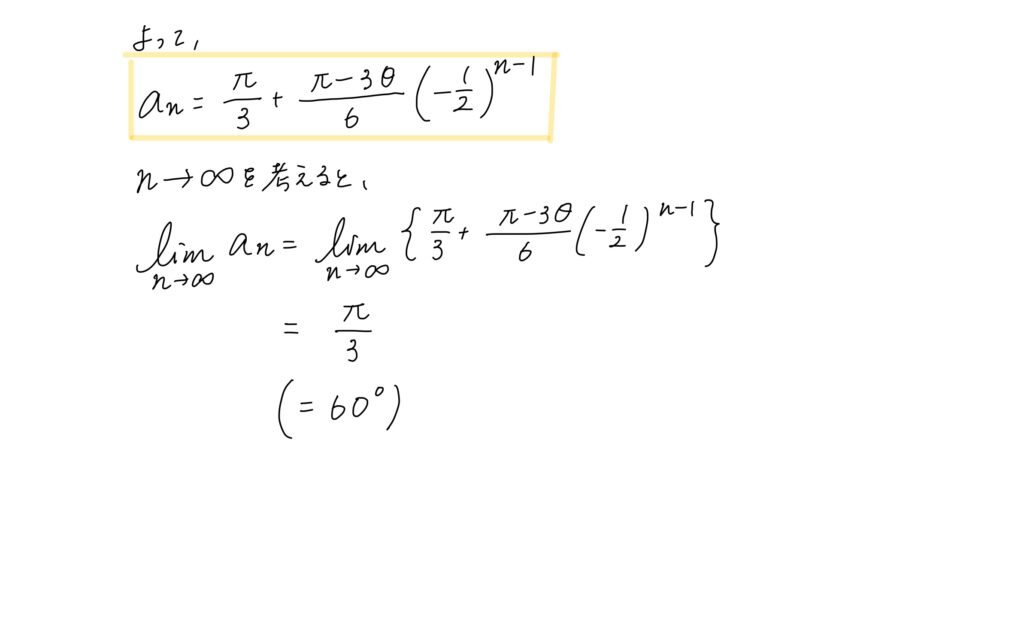
残り2つも同様にやればいいわけですが、考え方はほぼ同じなので、右角だけ計算してみます。
右角は同じ項が2つずつ出てきているので、同じものはひとまとめにして考えます。
n回目の操作後の右角の大きさをbnとした時、次のように極限を求めることができます。

こんな感じで同じように60°と出るわけです。
なので、残りの左角も60°であるということがわかります。
実は計算の手間を省くこともできる!?
直感で考えた時は、「あれ、意外と簡単?」と思えた問題でしたが、ちゃんと計算しようとすると結構面倒でしたよね。極限の計算練習にはもってこいですが・・・
3つの角を全部計算で求めるのはあまりにも非効率なので、もっと簡単にする定理を紹介します〜
それは、右角と左角は中央の角の部分列と捉える定理です!!!
部分列とは、数列{an}の一部の項を、もとの順番を保ったまま並べてできる数列のことです。
右角と左角で出てくる数は、真ん中の角の大きさの数列{an}の一部でしたよね。
なので、右角と左角の大きさの数列はどちらとも{an}の部分列ということです。
部分列について、こんな定理があります。
数列{an}が収束する数列で、その極限がαであれば、{an}の任意の部分列は同じ極限αに収束する。
つまり、{an}は60°に収束するので、右角と左角も60°に収束するよ、ということです。
この定理の証明は大学レベルの内容なので、サラッと概要だけ説明しますね。
意味わからんよ〜〜〜という方はすっ飛ばして構いません。
数列{an}がαに収束することの定義は、任意のε>0について、ある自然数Nが存在して、Nより大きい全ての自然数nにおいて|anーα|<εが成り立つこと。 数列{an}の部分列{an(k)}についてn(k)>kだから、k>Nの時、n(k)>N 従って|an(k)ーα|<εが成り立つ。よって、部分列{an(k)}はαに収束する。
この部分列の定理を使えば、極限の計算をしなくても3つの角がそれぞれ60°に近づいていくことを示すことができます。
真ん中の角がある角αに収束すると仮定する。この時、0<α<180°である。 左角と右角の大きさの数列は、真ん中の角の部分列なので同じくαに収束する。 左角、真ん中の角、右角の和は180°なので3α=180° よって、α=60°
定理を1つ知っているだけで、サラッと解けてしまいましたね。
直感では当たり前なことを証明するって意外と大変なのですよね。
そんじゃ、また。

コメント