最近、「無限〇〇」ってよく聞きませんか?
私はよく無限ピーマンを作ります。ピーマンを細切りにして、鶏ガラスープの素やごま油やツナと混ぜてチンしてできる簡単おかずでしかもめちゃくちゃ美味しい!
無限に食べられるから無限〇〇。”無限”ってワードがついたレシピは大体間違いなく美味しい、神ワードなんですよね〜
今日はそんな”無限”についてのお話したいと思います〜
※今回は池田洋介さん著「読むだけで楽しい 数学のはなし」を参考にしました。この本、数学が苦手な人でも、活字が苦手な人でも、数学の楽しさがわかるおすすめの一冊です。サラッと読めるけど、内容はちゃんと数学の要点を捉えていて、読書が苦手なさとあずも最初から最後まで楽しく読めちゃいました!
【無限の不思議①】有限の中に無限が存在する?!
ここで皆さんに問題です。
「正の数を無限に足していったら、その和は必ず無限になる。○か、×か。」
正解は❌!
簡単な例を見てみよう。
例えば、学校の掃除の時によく使っていたチリトリを思い出してみよう。
ホウキ係よりチリトリ係の方が動かなくて楽かな〜と思いきや、チリトリって結構扱い難しいと思うのは私だけではないだろう。
掃いても掃いても、床にゴミが残る。チリトリを少し後ろにずらしてもまだ残る・・・最後の方なんて、「もういいや!」とこっそり残りのゴミを床に馴染めせてみたり(笑)
そんな経験、みんな1回は経験したことありますよね?
これを数学っぽく考えてみる。
仮に、1回チリトリを使うごとに9割のゴミはチリトリに入り、1割は床に残るとする。
初めのゴミの量を1とすると、1回目は0.9のゴミがチリトリの中に入り、0.1のゴミが床に残る。
2回目は0.09のゴミがチリトリの中に入り、0.01のゴミが床に残る。
3回目は0.009のゴミがチリトリの中に入り、0.001のゴミが床に残る。
このように、永遠と1割のゴミは床に残り続けて、いくら掃いてもゴミは全部取れないのだ。
ここで、チリトリの中に入ったゴミの量に注目したい。
チリトリの中のゴミは、1回目は0.9、2回目は0.09、3回目は0.009・・・と無限の「回数」のごみが入ってくるわけだが、チリトリの中のゴミの「量」は無限になるわけではない。
何回チリトリの中にごみが入ってこようと、チリトリの中のゴミの量は1なのだ。
つまり、
1=0.9+0.09+0.009+0.0009+・・・
このように、チリトリの中のゴミの量は1に限りなく近づいていくが、1を超えることはないのだ。
つまり、正の数の無限の和が、有限の値1になる例が示されたわけである。
【無限の不思議②】「正の整数」と「正の偶数」はどっちが多い?
「正の整数」と「正の偶数」どちらが多い?と言われて、みなさんどのように答えますか?
正の整数には奇数と偶数が入っているんだから、偶数の方が数が多い!と考える人もいるだろう。
でも、「正の整数と正の偶数の数は等しい」という解答が正解なのである。
そこには「1対1対応」という考え方がある。
例えばコンサートに来た人の人数を知りたいとしよう。そのために、入り口に立って一人一人数えていくという手が一番原始的かもしれないが、大体の人はそんな非効率なことはしないだろう。入場券の半券を回収して、その枚数を数えればコンサートに来た人も人数がわかるからだ。これは、1人に1枚のチケットが対応するから、来場者数とチケットの枚数は同じになるだろうという考え方である。
このように、1対1対応の考え方は私たちが意識せずとも自然と使う考え方なのである。
今、2つの箱A、Bがあるとする。Aにはペン、Bにはペンのキャップがそれぞれ大量に入っているとする。(ペンもキャップも無限にあることを設定するので、もちろん箱の体積も無限にある、ドラえもんのポケットのようなものであるとしておこう)
Aのペンには、1、2、3、4・・・と正の整数、Bのキャップには2、4、6、8・・・と正の偶数が番号として振られている。
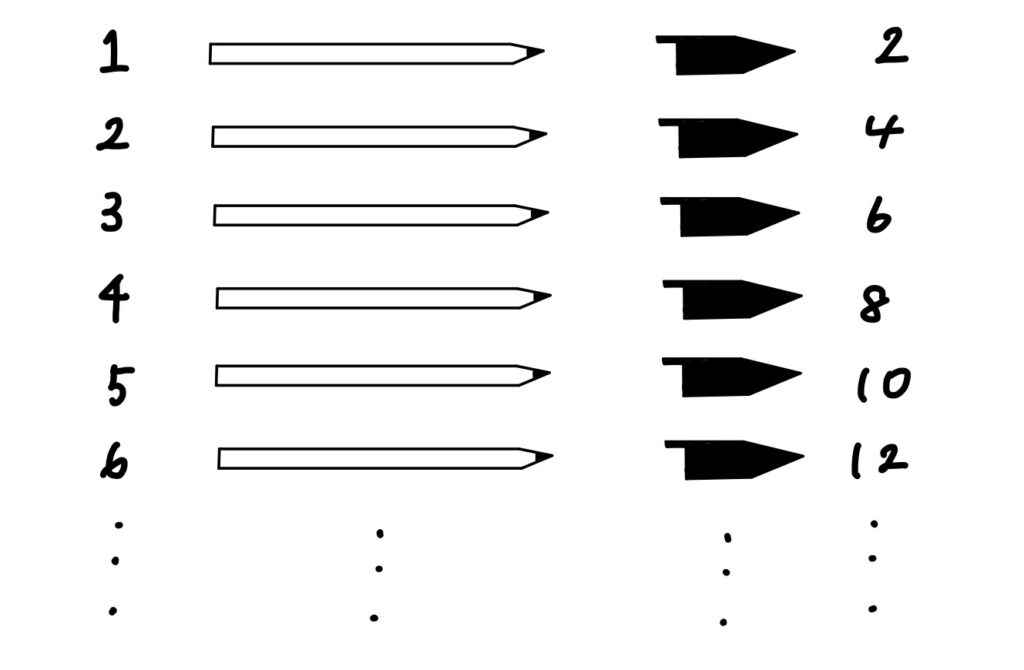
ペンにキャップを1つずつはめていく作業に取り掛かろう。
1番のペンには2番のキャップ、2番のペンには4番のキャップ、3番のペンには6番のキャップ・・・といった感じで、1つ1つはめていくと、どんなペンにもはめるキャップが存在するし、逆にどんなキャップにもはめるペンが存在する。
つまり、ペンの数とキャップの数は等しいということである。
「部分」の数は「全体」の数より少ないというのは有限の世界の中で起こっていることで、無限の世界では有限の世界の常識が当てはまらないことがこの例で示されたことになる。
ヒルベルトホテルのパラドックス
ここで、無限の世界の不可思議さを示すお話を紹介しよう。
ヒルベルトホテルという、無限の客室があるホテルがあった。
その客室には1、2、3・・・と番号が振られている。
ある日1人の旅行客が来て、今晩このホテルに泊まりたいと言われたが、あいにく今日は満室である。
旅行客ががっかりしていると、ホテルのオーナーがあることを思いつき、ホテルに次のような案内放送を流す。
「今晩ホテルにご滞在中のお客様、申し訳ありませんが、今お泊まりの客室番号に1を足した客室番号に移動をお願いします」
すると、1番の客室が空き、無事その旅行客は泊まることができたのであった。
そして次の日、その日も満室である。
そこに、バスツアーの無限人の旅行客がやってきて、今晩泊めてほしいといった。
そこでホテルのオーナーは次のような案内放送を流す。
「今晩ホテルにご滞在中のお客様、申し訳ありませんが、今お泊まりの客室番号に2をかけた客室番号に移動をお願いします」
すると、1号室のお客さんは2号室へ、2号室のお客さんは4号室へ、3号室のお客さんは6号室へ・・・と偶数番号の客室に移っていき、奇数番号の客室は空いたため、無事に無限人の旅行客はそのホテルに宿泊できたのである。
これで今晩のホテルは大儲けできただろうと考えるのは、有限の世界で考える私たちの浅はかさである。
なぜなら、無限人の客を新たに入れようが入れまいが、その売り上げ金額は「同じ」なのだから。
【無限の不思議③】無限より大きい無限がある・・・?
無限に大きさはあるか。
もし無限に大きさがあるのなら、2つの無限の大きさを比べることができる。
そして、どちらか一方がもう一方より大きい無限であるということができる。
そんなことありえるだろうか?
実際に具体例で考えてみよう。
今、囲碁の石を白と黒をそれぞれ大量に用意して、それらを一列に並べることを想定してみる。
全て同じ色で並べてもいいし、白と黒を交互に並べてもいいし、規則性なく並べてもいい。
とにかく、1列に並べてみると、下の図のように白と黒が無限に並んだ列(「白黒列」と呼ぶ)ができる。
○●●○○●○○○・・・
もちろん、白黒列の種類は無限に存在する。
今、先程の白黒列を1番とし、他の白黒列を2番、また他の白黒列を3番、という感じで「正の整数」を対応させていく。

もし、このような対応表が作れるのであれば、「白黒列」の数と「正の整数」の数は同じであると言える。
逆に、対応表が作れなければ、2つの無限のどちらかが多い、つまり無限より大きい無限が存在すると言える。
「無限より大きい無限」と聞いて、頭の中に「?」がたくさん浮かんだ人も多いでしょう。
この問題に対して、ドイツの数学者カントールは「対角線論法」という方法を使って、「白黒列」と「正の整数」の対応表を作ることはできないことを証明した。
今、仮に全ての白黒列が正の整数に対応できたとする。
ここで、図のような対角線上の白黒列に注目する。

この対角線上も、白と黒が無限に並ぶ列なので、1つの白黒列である。
この対角線上の白黒列の白と黒が入れ替わった列を考えてみよう。
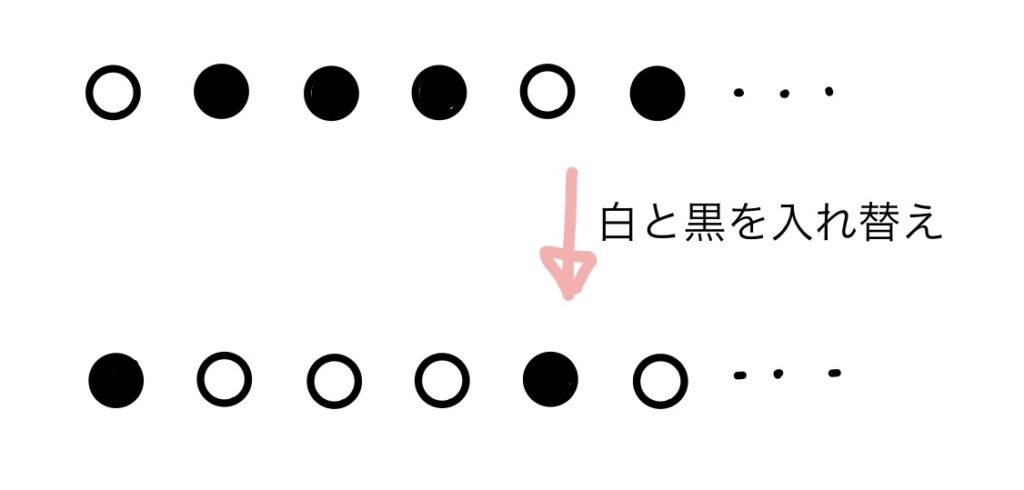
これも同じく白黒列の1つである。
実は、この白黒列は正の整数に対応させたどの白黒列とも一致しない。
なぜなら、新しい白黒列は1番目の白黒列とは少なくとも1個目の白黒が異なるし、2番目の白黒列とは少なくとも2個目の白黒が異なるし、3番目の白黒列とは少なくとも3個目の白黒が異なる。
このように、新しい白黒列は正の整数と対応させたどの白黒列とも一致しない。
つまり、白黒列の数は正の整数の数より多いことが証明されたのだ。
このことから、無限より大きい無限が存在することが示されたのだ。

コメント