こんにちは!さとあずです。
今回は正多面体を折り紙で作ってみたので、その作り方をご紹介します。
先日多面体のお話をしたときに、「ポリドロン」という多面体を作れるパズルをご紹介したのですが、今回は「折り紙で作れたら誰でも気軽に立体を楽しめるんじゃないかな?」と思い、作ってみることにしました!!
目標は5種類の正多面体を作ることですが、まずは面の形が正三角形である正四面体、正八面体、正二十面体から作ってみましょう〜!
切頂二十面体のお話
※今回は、阿部恒さん著「すごいぞ折り紙」を参考にしました。
正多面体についておさらい
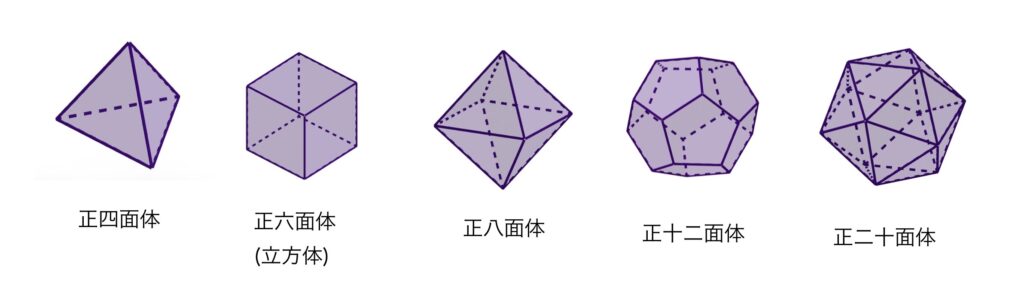
正多面体の定義は「全ての面が同じ正多角形(正三角形or正方形or正五角形)でできており、かつすべての頂点において接する面の数が等しい凸多面体」です。
正多面体は「正四面体、正六面体、正八面体、正十二面体、正二十面体」の5つしかありません。
用意するもの
正方形の折り紙
ハサミ
テープ
1:√3の長方形を作ろう
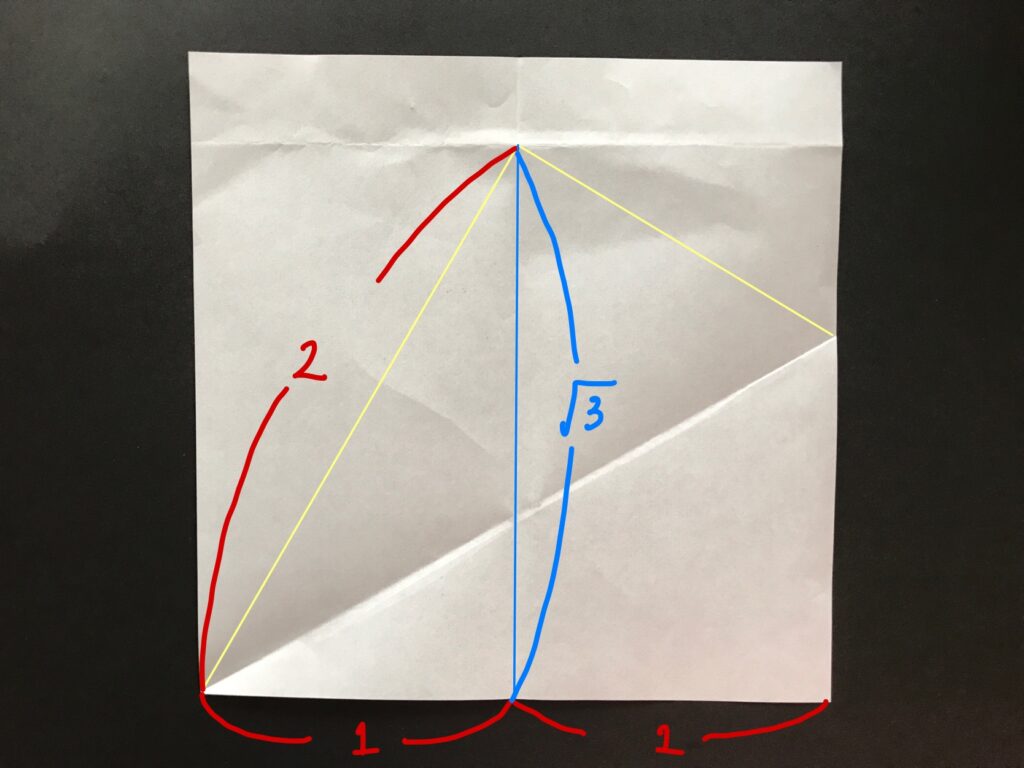
まず、正三角形ユニットを作るために、1つの正方形の折り紙から2つの長方形を作ります。



※1:√3になる理由としてはこの図を参照してみてください。
正三角形ユニットを作ろう
今回は、全ての面が正三角形の多面体を作るので、正三角形ユニットをひたすら折って、あとは組み合わせればできます!
正三角形ユニットはユニットAとユニットBの2種類作ります
⦅ユニットAの作り方⦆













⦅ユニットBの作り方⦆

あとは、ユニットAの作り方と同じ!

下の図のように、ユニットの内側の2つの三角形が正多面体の面になるイメージだよ!
端の2つの三角形は隣のユニットに差し込むのにつかうよ!

正四面体を作ろう
ユニットAとユニットBを1枚ずつ用意します。(生四面体なので面が4つだからユニットは2枚!)

こんな感じで差し込んで・・・

隣あう三角形に差し込んで・・・
完成!!(うまく説明できないのではしょりました(笑))


テープを使わなくても綺麗にはまったよ〜!
正八面体を作ろう
ユニットAを4枚またはユニットBを4枚用意します。(同じものを4枚!)

図のように差し込んで・・・

他も図のように差し込んで・・・

黄緑とオレンジもくっつけて・・・半分完成。

もう半分も同じように組み合わせて、完成!


これもテープなしでも、綺麗にできたよ〜!
正二十面体を作ろう
ユニットAとユニットBを5枚ずつ、計10枚用意します。

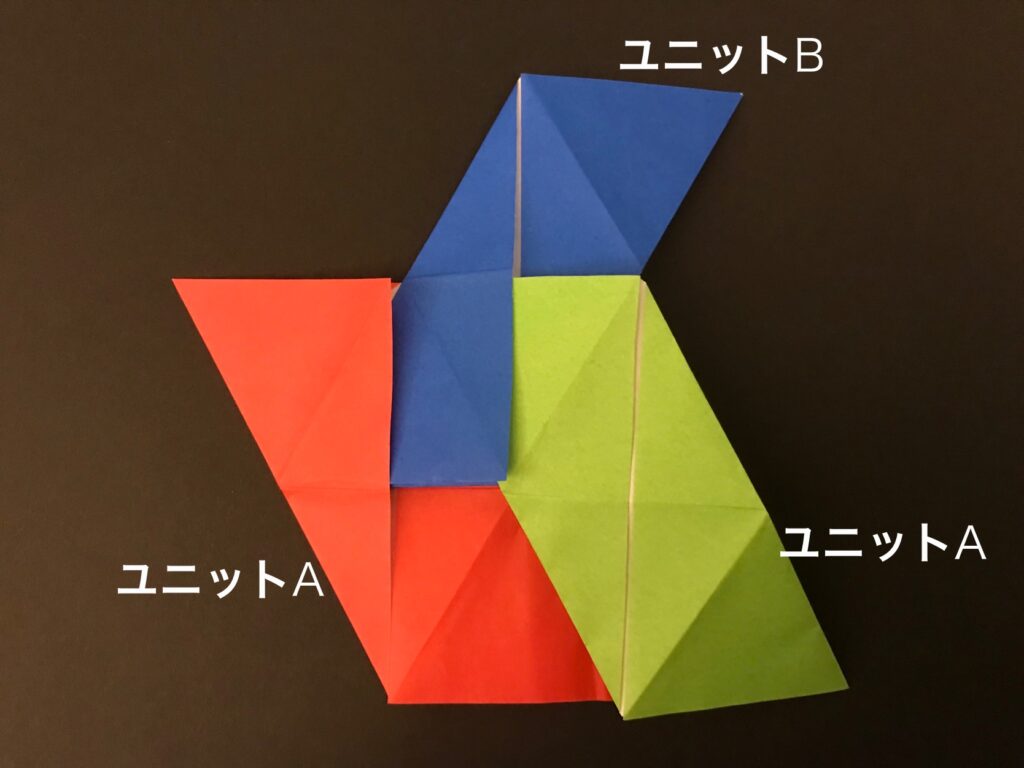

こんな感じで差し込んでいきます。
ユニットAとユニットBが隣り合うように差し込んでいくと・・・
完成〜〜!!


これは裏にテープで固定していかないと崩れてしまうので、テープは必須!
正二十面体は1つの頂点に5つの面が集まっているということを意識しながら組み合わせていくとうまくできるよ〜!
実際作ってみた感想
折り紙での正多面体の作り方って色々あると思うんだけど、これのいいところは同じユニットを使って3種類の正多面体が作れちゃうところ!
1つのユニットから2つの面ができるというところも、何個のユニットを使えば作りたい多面体が作れるか予想しながらできるのが、この作り方の大きな魅力だと思いました!!
実際に作ってみて、「1つの頂点に何個の正三角形が接すればいいんだっけ〜?」とか考えながら作るので、正多面体の性質を作りながら学べるのもすごくいいなと思いました。
何より、折り紙で実際に作ってみて、実物をみて立体のイメージができるのがいいですよね。
あえて注意点を挙げるとすれば、今回いろんな色の折り紙を使ってしまったので、1つの面が2色になってしまってちょっと見づらくなってしまったところでしょうか・・・一色で作った方が立体のイメージがつきやすいかもですね。
次は、立方体、正十二面体にもチャレンジしてみたいと思います!!
それでは!

コメント