早速ですが、問題です。
全く同じ2つのコインA、Bを用意します。(100円玉2枚でも、500円玉2枚でも円の形をしていればOK) 2つのコインを図のように隣り合わせに置き、コインBを固定して、コインAをコインBの周りに滑らないように転がして、一周させて出発点まで戻します。コインAは何回転するでしょうか?
コインBは何回転するでしょうか?
さて、今回はこの問題を出発点にして思考を巡らせていきましょう〜!
円の周りに円を回転させると予想外の結果が!?
さて、先ほどの問題をみて、次のような答えを出した方がいるのではないでしょうか?

2つの円(コイン)の円周の長さは等しいから、コインは1回転する。
私自身も最初こう考えました。
この問題はコインが2枚あれば簡単に実験できるので実際に実験してみてください。
すると、あれ?コインBは2回転しているじゃありませんか!
2つのコインの円周の長さは等しいはずなのに、なぜかコインは2回転する。
不思議ですね〜
答えの前に、もう1つ似たような問題をやってみましょう!
円Bの半径は円Aの半径の3倍。円Aを円Bの周りに滑らないように転がして、一周させて出発点まで戻してくる。円Aは何回転するか?
これも、円Bの円周の長さは円Aの円周の長さの3倍なので、3回転すると答えたくなってしまいますが、先ほどの問題からこの考え方は❌ですよね。
同じ大きさの円の時2回転だったから、3倍の円の周りだと6回転?なんて考える人もいるかもしれませんが、答えは4回転。
つまり、固定している円Bの半径が回転する円Aの半径のn倍の時、円Aはn+1回転するんです!
実は先程の2つの目の問題はアメリカの大学入学試験SATでも出題された問題です。
SATの出題者も3回転だと思って出題したようで、選択肢に「4回転」がなく誰も正解できなかったそうです。
後日、間違いが明らかになって、ニューヨーク・タイムズとワシントン・ポストで報じられたそうです。
なぜ1回転増えるの?
計算から入ってしまうと混乱が生じるのでまずは直感的に理解してみよう。
1問目の問題がもし、次のような問題文だったらどうだろう?
円Bの円周と等しい長さの直線上を、円Aは何回転するか?
これだったら、答えは1回転ですよね。
しかし、円が別の円の周りを転がるときは、自分自身が回転すると同時に、固定された円の周りを回転するので、固定された円の周りを転がる1回転分が余計に回転して1+1の2回転になったわけです。
なんだかよくわからないぞ?という方のために、もう少し噛み砕いて説明します。
下の図は、円を直線上に1回転した時の図です。
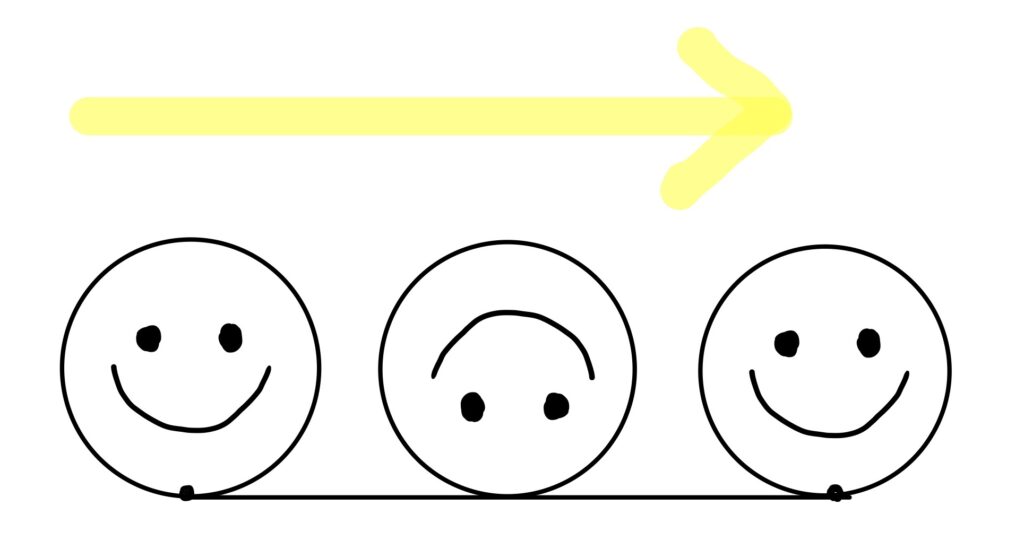
円を1回転させた時、円が転がった線分の長さと円周の長さは等しいですよね。
試しに、線分のちょうど真ん中(円が半周した部分)で直線を切り取り、線分を半円の形にしてみましょう。

すると、円が半周したとき、直線上ではコインは下向きになっていますが、線分を半円にするとコインはスタートの時と同じ向きになっています。
つまり、円が半周して、さらに固定された円の周りも半周しているので、その結果半分進んだ時点で1回転したということです。
計算でさらに詳しく証明してみよう
直感的に1回転増えることは分かっても、でも本当にそうなのかわからない〜!という方のために、計算でも証明してみます。
円Bの半径は円Aの半径のn倍。円Aを円Bの周りに滑らないように転がして、一周させて出発点まで戻してくる。この時、円Aはn+1回転することを示してみます〜!(nは自然数)
円Aが1回転するのに必要な円 Bの中心角をθとする。(つまり、2π÷θの計算結果がそのまま円Aの回転数になる。2π÷θ=n+1になることを示していくよ〜)
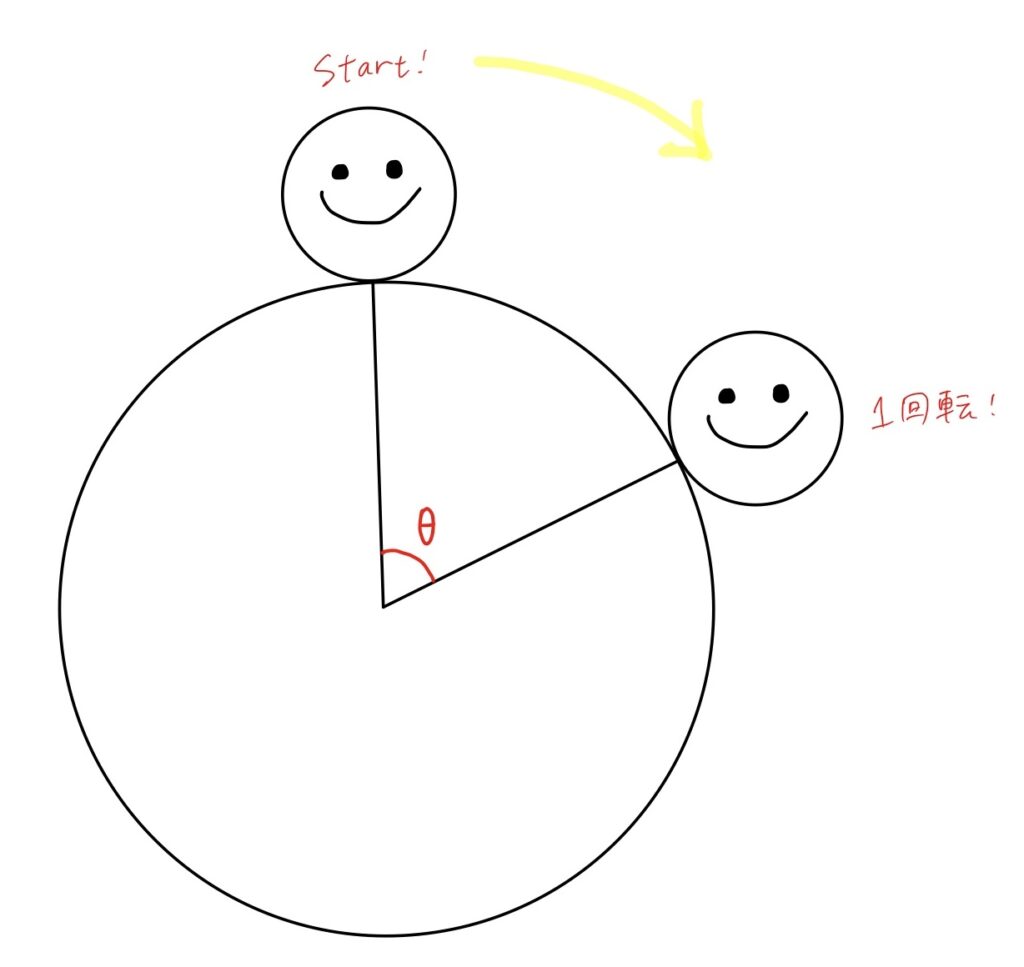
円Aの半径を1とすると、円Bの半径はn
円Aが1回転した時に通る円Bの円周の長さはnθ
長さnθの線分lを円Aが転がすことを想定すると、円Aが回転する角度はnθ
さらに、円Bの円周上を転がる場合、さらにθだけ回転するので
円Aが1回転する角の大きさはnθ+θ=(n+1)θ
これが1回転つまり2πと等しいので(n+1)θ=2π
両辺をθで割ると、2π÷θ=n+1 (証明終わり)
いかがでしたか?
一見簡単に思える問題でしたが、予想外に考えさせられる問題でしたね。
それではまた。

コメント