こんにちは!さとあずです。
突然ですが、皆さんに質問です。
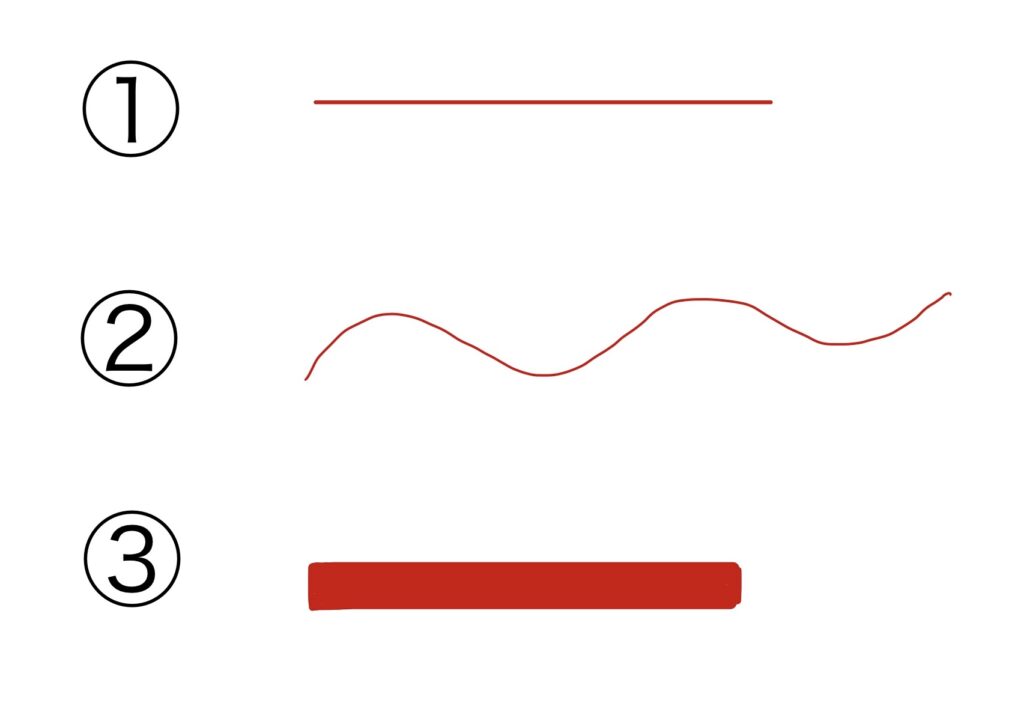
次の3つの中で、「線」はどれでしょう。
正解は・・・
どれも「線」ではありません!!

え、どういうこと〜〜?
①はまっすぐな線だし、②は曲がった線、③は太い線だし、全部「線」だと思った〜

そう見えるよね。
でも厳密にいうとどれも「線」ではないんだ。
そもそも「線」って何だと思う?

え、線?何かっていわれても・・・
そんなイジワルな質問しないでよ〜〜〜(泣)

ごめんごめん。
図形を描くときに当たり前のように使っている「点」とか「線」って何かなんて考えたことないよね。
でも、その定義って紀元前、つまり2000年以上前にはすでに考えられていたんだよ。
今回は、図形を扱う上で必ず扱う「点」や「線」って何?というお話を、「ユークリッド原論」という数学の著書に基づいて書いていきます。
これを読んで、「へぇ〜〜ちょっと賢くなった気がする!」と思っていただけたら、とっても嬉しいです。
ユークリッド原論とは?
紀元前3世紀ごろに古代エジプトの数学者エレクレイデスによって編纂されたといわれる数学書。
古代ギリシアの哲学者プラトン(ソクラテスの弟子、アリストテレスの師範)の学園アカデメイアで知られていた数学の成果の集大成となっていて、数学における命題・公理・定理が体系的にまとめられています。
この約2300年前に作られた本が、今日までの数学の発展に大きく影響していて、数学史を語るには避けて通ることのできない名著です。
さとあずも何度か図書館で借りて翻訳本を読んでみたことがありますが、確か5センチくらいの厚さでかなりのボリューム感があって、表紙もすごい歴史を感じさせる1冊で、持ってるだけで頭が良くなった気分になれました(笑)
そんないらない話はさておき、当時はまだ今のような数の概念も定まっていない時代だったのにも関わらず、ここまで数学の知識を体系的に書けちゃう当時に方々の知能の高さに圧巻される1冊です。(語彙力がなくて申し訳ない)
今回は、その本の中で一番最初に書かれている「点」と「線」のお話を紹介したいと思います!
「点」って何? 「線」って何?
「ユークリッド原論」の一番最初に「点」の定義が次のように書かれています。
定義1 「点は部分をもたないものである」
意味わかりますか?1行目からもうやめたくなる訳のわからなさですよね。
すごーく噛み砕いて解釈すると、例えば「・」のような私たちが普段「点」だと思っているものは、目に見えているのでその時点で「点」ではないということです。「部分をもたない」つまり、「目に見えない」ということです。
次に「線」について書かれている定義2と定義3を見ていきましょう〜
定義2「線には幅はなく、長さがある」
定義3「線の端は点である」
一番最初の3つの中で線はどれでしょう問題で、どれも線ではないという話をしましたが、なぜ「線」ではないというと、3つとも「幅」があったからです。
目に見えてる時点で、太さがある訳なので、幅がありますよね。
だから、厳密にいうと「線」ではなく、「線っぽいけど線じゃないもの」なんです。
うわ〜〜すごい屁理屈〜〜って思うかもしれませんが、こうやって厳密に前提を決めていかないと、後々矛盾が起きてしまうことも多いので、この厳密さが数学という学問の中でとっても大事なんですよね。
私たちが紙にペンで書いていた点や線は、「本当はかいて表現することはできないけど、それをあえてかくとこんな感じで表せるかな〜」みたいな感じでしょうか。
「線には幅(太さ)がない」というのはとても大切な考え方で、例えば「次の三角形の面積を求めよ」という問題があったとします。(各辺の長さや高さなどはわかっているとします)

求められそうですか?
これを見て、「いやいや、辺が極太すぎてどこの面積出せばええねん!」って思った方は、もうユークリッド原論の線の定義はばっちりなはず👍
どんなに細く線を書いても、書いた時点で拡大すれば太さがあるので上の三角形のように面積が出せなくなってしまいますよね。
ちなみに、定義4には直線、定義5・6には面、定義7には平面について言及されています。
定義4 「直線とは点がまっすぐに並んだ線である」
定義5 「面には長さと幅だけがある」
定義6 「面の端は線である」
定義7 「平面とは直線が平らに並んだ面である」
ここで大事なことは、「直線は点がまっすぐ並んでできた線」「平面は直線が平らに並んだ面」であるということ!!
イメージはこんな感じ!
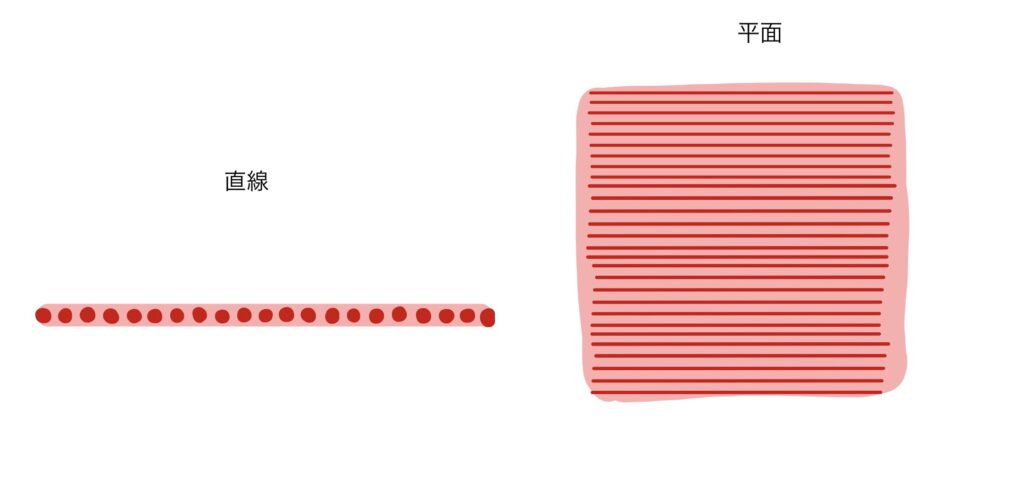
正確には、直線は無数(無限個)の点が隙間なく集まっているので、あくまでもイメージです。
直線は点からできていて、面は直線からできているんだから、つまり面は点からできているとも言える。
この考え方って、数学でみんながよく学ぶ関数のグラフの考え方だったり、高校数学でたくさんの人がつまづく軌跡や微分法や積分法に通ずる大事な考え方なんですよ〜。
知ってて損はしないかも?!?!
そんじゃ今回はこの辺で!


コメント