こんにちは!さとあずです。
今回は、私たちが生活する上で欠かせない「お金」についてのお話です。
※今回は池田洋介さん著「読むだけで楽しい 数学のはなし」を参考にしました。この本、数学が苦手な人でも、活字が苦手な人でも、数学の楽しさがわかるおすすめの一冊です。サラッと読めるけど、内容はちゃんと数学の要点を捉えていて、読書が苦手なさとあずも最初から最後まで楽しく読めちゃいました!
金利0.1%で1万円預けるといくら増える?
今のおじいちゃんおばあちゃんが若い頃は銀行の金利は5%や8%も珍しくはなく、利息で生活するのも夢ではなかったようですが、今や銀行の金利は0.1%を切ることも多いですよね。
ここで仮に元金1万円を年金利0.1%で5年間預けることを想定します。
1年目には1万円に0.1%の利息がつくので、1.001(万円)
2年目に1.001万円に0.1%の利息がつくので、1.001×1.001(万円)
同様に5年目の金額を計算すると、1.001×1.001×1.001×1.001×1.001=1.0015(万円)
これを計算するには電卓が必要ですが、大まかな金額なら簡単に計算する方法があります。
それは、小数点以下の部分に累乗の数字をかけてしまえばいいんです。
つまり、1.0015≒1.005
実際に電卓で計算すると、1.0015=1.00501001001なのでほぼほぼ同じ値です。
この計算方法は、利率が低いときに使うことができます。
例えば、元金1万円を年金利0.2%で10年間預けた場合、1.00210≒1.020(万円)、つまり200円の利息がつくと計算できます。(実際、1.00210=1.020180963368なので約201円で誤差は1円だけ)
一般に、hが1やnに対して十分小さい時、次の式が成り立つから!
(1+h)n≒1+hn
詳しい理由は、後述(※)します。
左辺の(1+h)nは毎年(1+h)倍されていくことを示しています。例えば、h=0.001だったら、1年目は(1+0.001) (万円)、2年目は(1+0.001)2(万円)といった感じです。
右辺の1+hnは毎年hずつ一定に増加していくことを示しています。例えば、h=0.001だったら、1年目は1+0.001×1(万円)、2年目は1+0.001×2(万円)といった感じです。
左辺の金利のつき方を「複利」、右辺の金利のつき方を「単利」と言います。
つまり、この式は、金利が低ければ、最初の数年は複利と単利では大きな違いがないということを表しています。
具体的に言うと、金利0.1%の銀行に1万円を寝かし続けることは、年間に0.001万円つまり10円を追加していることと同じだということですね。
もっと具体的にいうと、金利0.1%の銀行に1万円を置いておけば、1年に1本うまい棒がもらえるということですね。(でもうまい棒って値上げされたんですよね・・・)
(※)関数f(x)がx=aで微分可能である時、x=aの近くにおけるf(x)の1次の近似式を求めます。
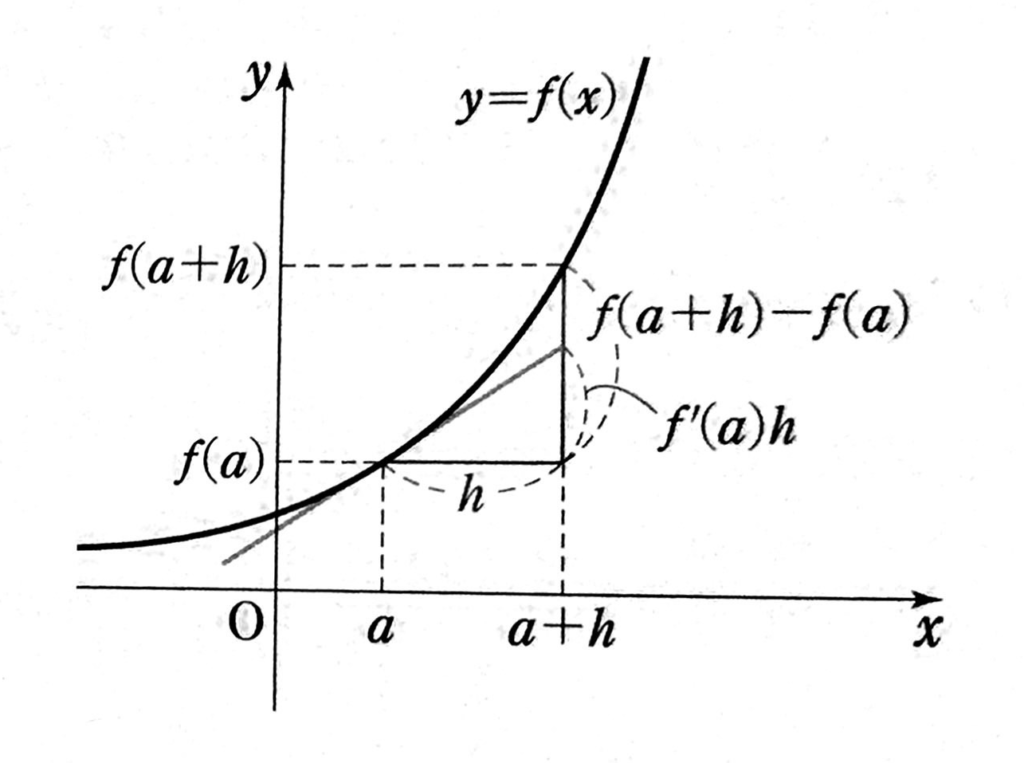
1次の近似式とは、曲線y=f(x)上の点において、x=aの近くでy=f(x)のグラフに近い形をしている直線のことです。
その直線は結果的には、曲線y=f(x)のx=aにおける接線のこと指します。
つまり、x=aの周りではy=f(x)の曲線と、x=aにおける接線が”ほぼ同じ”形をしているので、hがめちゃくちゃ小さい値ならx=a+hをそれぞれに代入しても、”ほぼ同じ”値になるよね、ということです。
接線の方程式は、点(x,y)=(a,f(a))を通り、傾きがf'(a) (これを微分係数といいます)なので、
y=f'(a)(x-a)+f(a)
と表すことができます。
y=f(x)の曲線と、x=aにおける接線にそれぞれx=a+hを代入するとほぼ同じ値になるので、
f(a+h)≒f'(a)h+f(a)が成り立つことになります。
今回はf(x)=xnとし、a=1すなわちx=1の近くにおけるf(x)の近似式を考えているので、実際に代入してみましょう。
ちなみにf'(x)=nxn-1なので、
左辺=f(1+h)=(1+h)n
右辺=f'(1)h+f(1)=nh+1
すなわち、(1+h)n≒1+hnが成り立つということです。
複利計算は等比数列の和を使えばいい!
実際にお金を貯めよう!と考えている人は、定期的に〇〇円貯めていこう!と考える人も多いですよね。
ここでは仮に、年に1万円ずつ金利0.1%の銀行に10年間預けることを想定してみましょう。
計算を簡単にするために、年の初めに1万円を積み立てて、年末にそれまでの貯蓄額に0.1%の金利がつくと想定します。
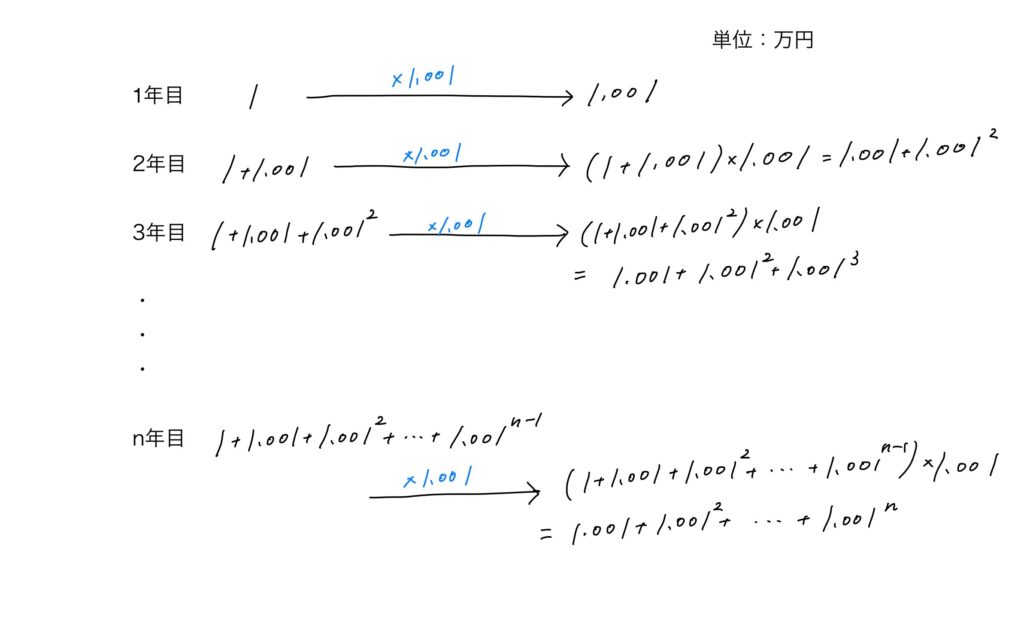
これだと小数点があって分かりづらいので、r=1.001と置き換えると、n年目の年末には r+r2+r3+・・・+rn だけ口座に貯まっていることになります。
これは、次の項にいくにつれてrずつかけているので、等比数列の和を計算することになります。
1つ1つの項を計算して足していくのはとっっても面倒なので、ちょっとした裏技を使っていきましょう。
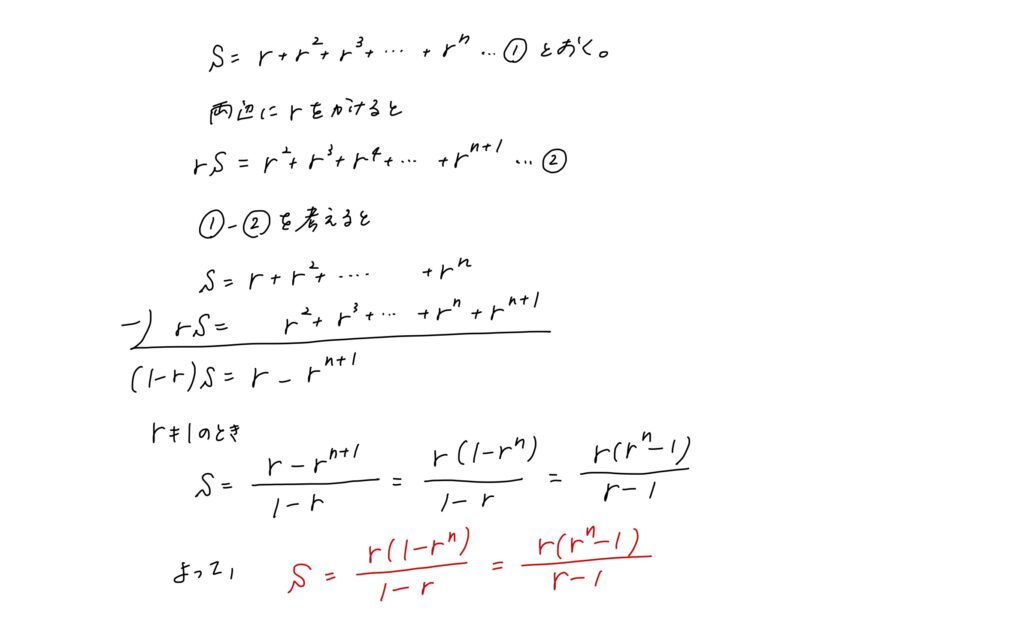
この計算方法は、等比数列の和を求めるときによく使われる手法です。
これを使って、10年目の貯金額を計算していきましょう。
r=1.001、n=10を代入すればいいので、
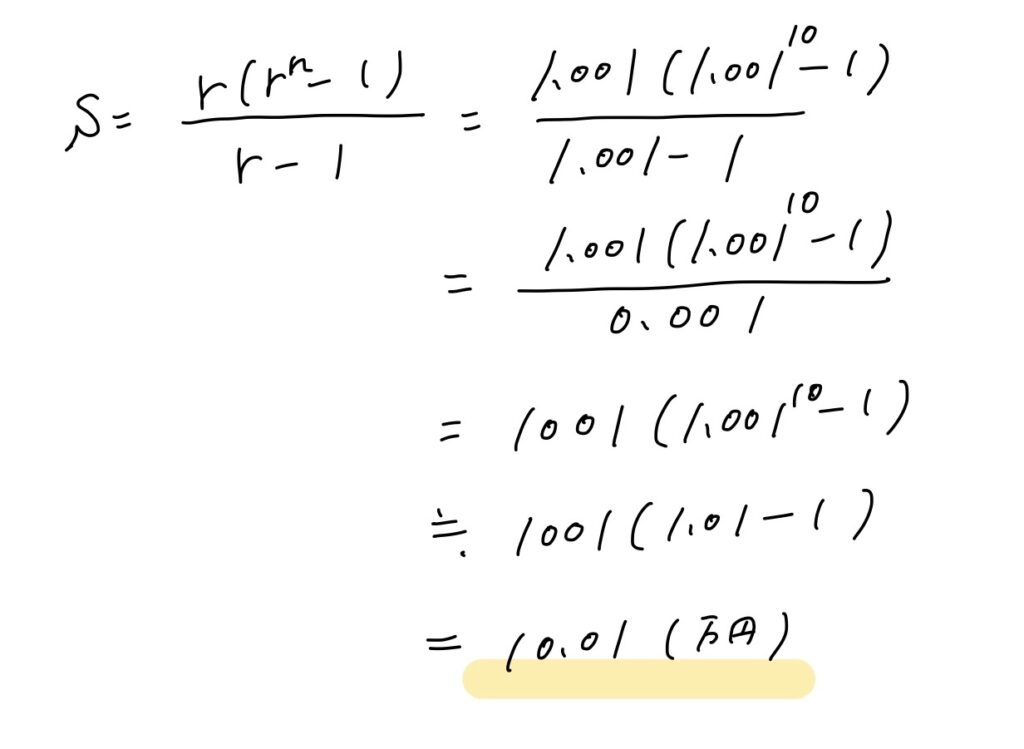
10年目には10.01万円、つまり10万100円になるということですね。
1万円を10年間金利なしで貯めると10万円になるので、約100円の利息がつくことになります。
10万円頑張って積み立てて、たったの100円か・・・やっぱり銀行に預けても全然お金が増えないのは計算しても明らかですね。実際の銀行はもっと金利が低いですしね。
ちなみに、年に1万円じゃなくて年3万円ずつ積み立てる場合を計算するには、全体に3をかければいいので、利息は300円になります。
また、月1万円ずつ積み立てるとなったら、年間に12万円積み立てることになるので、利息は1200円となります。
また、他の金利のバージョンや、年数を変えて計算するには、rやnの値を変えていけばいいだけですよね。
ちなみに他のパターンも計算したらこんな結果になりました。
金利を増やすと爆発的に増えていきますよね。
資産形成を考えるときに、金利を意識するかしないかが大きな別れ目になるのは表を見ても明らかですね。
ちなみに、こんなケースの場合も考えてみましょう。

年利4%で20年後に400万円貯めたいな〜!毎年いくらずつ積み立てていけばいいんだろう?
今回はr=1.04、n=20で計算すれば良いことになります。毎年の積立額をx(万円)であるとすると、
このことから約13万円ずつ積み立てれば年利4%で20年後に400万円貯められることになりますね。
実際13万円×20年=260万円の元金で400万円貯められるわけですから、金利の力、そして時間の力は大きいですね。
ちなみに、1.0420をサラッと計算していましたが、先ほどでた(1+h)n≒1+hnを使ってしまうと誤差が大きくなってしまうので電卓を使いました。。。
1.04を20回もかけると途中で何が何だかわからなくなってしまうので、iPhoneをお使いの方は実は裏技があります。
電卓の画面を開いて、画面を横向きにすると・・・(画面縦向きのロックはオフにしてくださいね。)
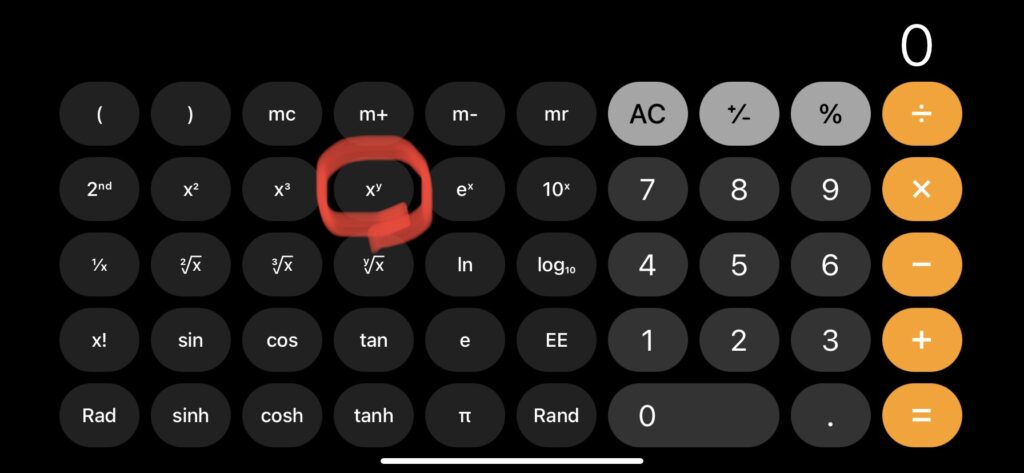
こんな感じでキーが増えます!
あとは、「1.04と入力 → xyを押す → 20と入力 → =を押す」であっという間に計算できます!
それでは!

コメント