こんにちは!さとあずです。
突然ですが皆さん、
3つの辺の長さが全て異なる不等辺三角形が、二等辺三角形であることがあり得ると思いますか?
「いや〜、そんなのありえないでしょ?」
ほとんどの人がそう思うんじゃないでしょうか。
でも、次の考え方が正しいとすれば不等辺三角形が二等辺三角形であるといえてしまうんです。
あなたはこのパラドックス、見破れますか?
それでは早速行ってみましょう!!
不等辺三角形は二等辺三角形!?
不等辺三角形ABCの∠Aの二等分線と、辺 BCの垂直二等分線の交点をOとする。
Ⅰ.点 Oが△ABCの内部にある場合
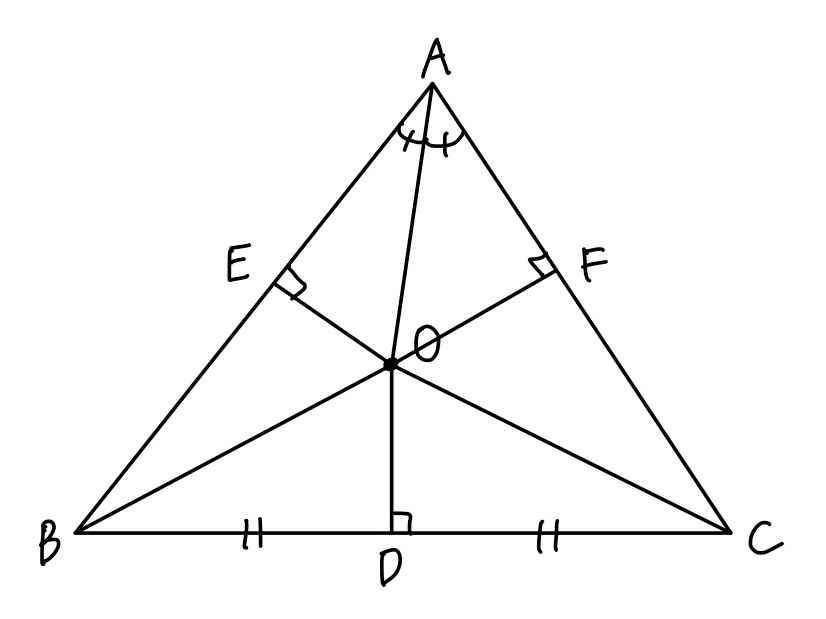
点Oから辺AB、ACにそれぞれ垂線OE、OFをおろす。
線分BCの垂直二等分線上の点は2点 B、Cからの距離が等しいのでOB=OC・・・①
△AOEと△AOFは∠AEO=∠AFO=90°の直角三角形で、OAは共通(斜辺)、∠OAE=∠OAFより、直角三角形の斜辺の1つの鋭角がそれぞれ等しいので合同である。・・・②
△OBEと△OFCは∠OEB=∠OFC=90°の直角三角形でOB=OC(①)、OE=OF(②)より、直角三角形の斜辺の他の一辺がそれぞれ等しいので合同である。・・・③
従って、②よりAE=AF、③よりBE=BFが言えるので、AB=AC
よって、△ABCは二等辺三角形である。
Ⅱ.点 Oが△ABCの外部にある場合
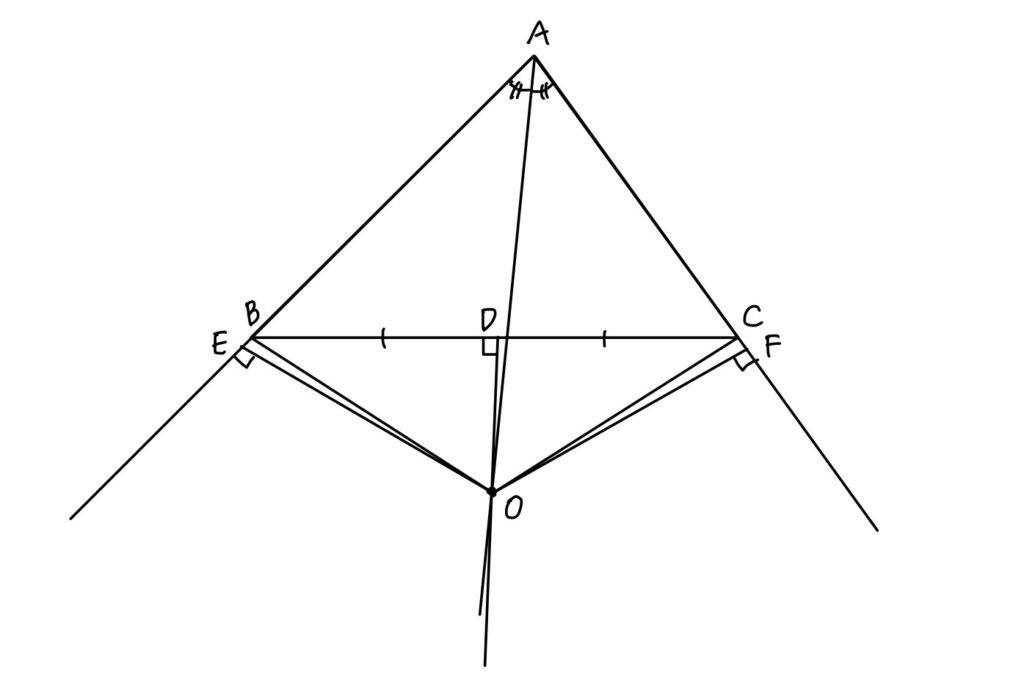
先ほどと同じように、ODは線分BCの垂直二等分線よりOB=OC・・・④
△AOEと△AOFは∠AEO=∠AFO=90°の直角三角形で、OAは共通(斜辺)、∠OAE=∠OAFより、直角三角形の斜辺の1つの鋭角がそれぞれ等しいので合同である。・・・⑤
△OBEと△OFCは∠OEB=∠OFC=90°の直角三角形でOB=OC(④)、OE=OF(⑤)より、直角三角形の斜辺の他の一辺がそれぞれ等しいので合同である。・・・⑥
従って、⑤よりAE=AF、⑥よりBE=BFが言えるので、AB=AC
よって、△ABCは二等辺三角形である。
この矛盾の正体は?
∠Aの二等分線と、辺BCの垂直二等分線の交点Oが△ABCの内部にある場合、外部にある場合を考えましたが、どちらもAB=ACの二等辺三角形になってしまいました。
でも、もしAB=ACの二等辺三角形ならば、∠Aの二等分線と、辺BCの垂直二等分線は一致するのでそもそも点Oがありません。
「ABとACは等しくはない」という前提から始まらなければ点 Oはできないのに、点 Oができる前提で話を進めるとAB=ACになってしまう、、、という矛盾が起きてしまいました。
さて、なぜこんな不思議なことが起きてしまったのでしょうか。
それは・・・
簡潔にいうと、「そもそも図がおかしい」のです。
先ほど提示した図をもう一度見てみましょう。
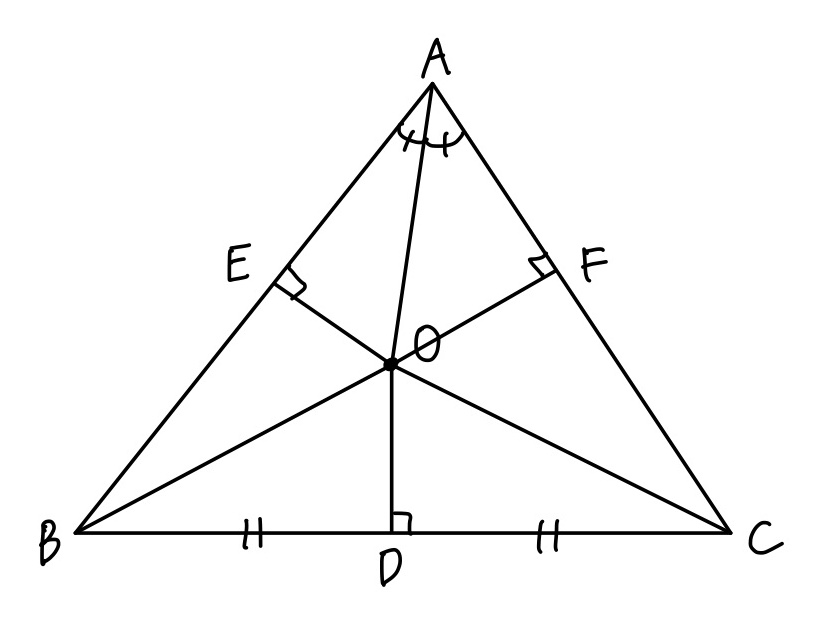
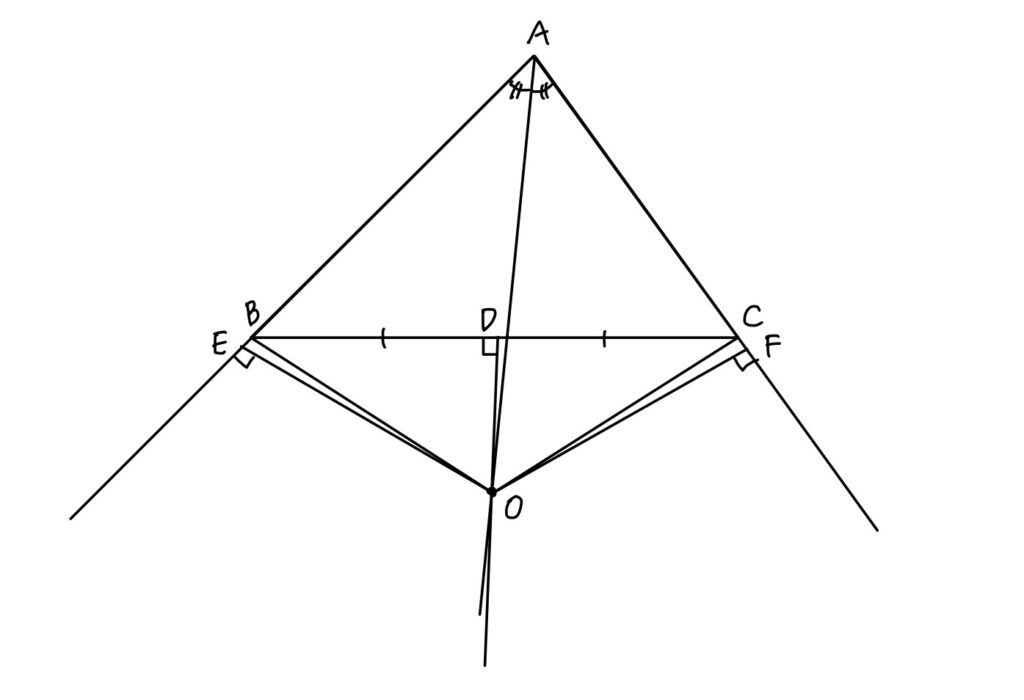
ん?なんか歪んでない?
そうなんです、歪んでいるんです。
これはさとあずの図が下手くそなのではなく、歪むべく歪んでいるんです。
まず、そもそもなんですが、点Oが△ABCの内部に来ることはあり得ません!
なぜでしょう?
今、AB>ACであるとしましょう。
この時、点Aは辺BCの垂直二等分線よりも右側にあります。
∠Aの二等分線と辺 BCの交点をGとすると、”角の二等分線と線分の比”より BG:GC=AB:ACなので、AB>ACのとき、BG>GCとなります。
一方、点Dは辺BCの中点なので、点Gと点Dの位置を比べると、点 Gの方が中点Dよりも右側にあり、下の図のようになります。
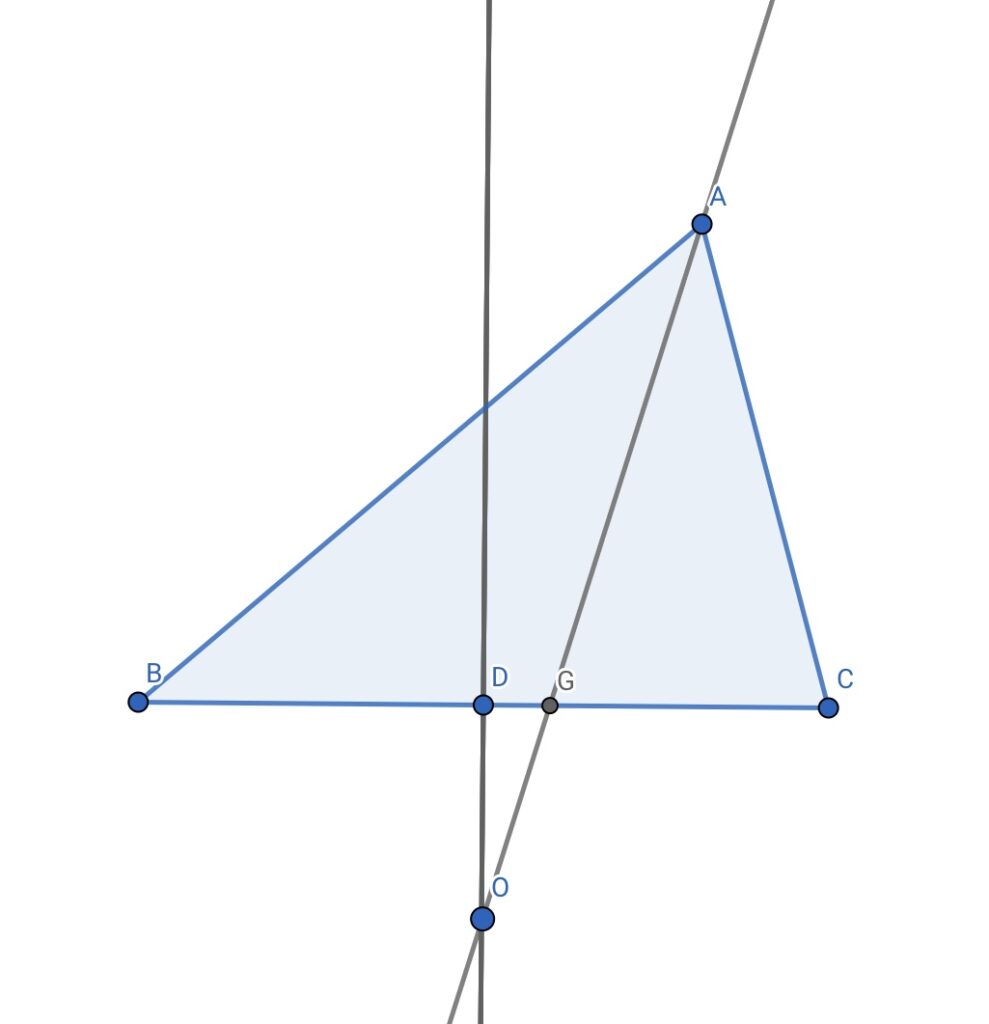
このように、∠Aの二等分線が△ABCの内部にある時、常に辺BCの垂直二等分線の右側にあり、△ABCの内部で交点を持つことはあり得ません。
AB<ACの時も同様のことが言えます。
従って、パターンⅠの点Oが△ABCの内部にある場合はそもそもあり得ないということになります。
では、パターンⅡはどうでしょうか。
パターンⅡを正確に描くとこんな感じになります。
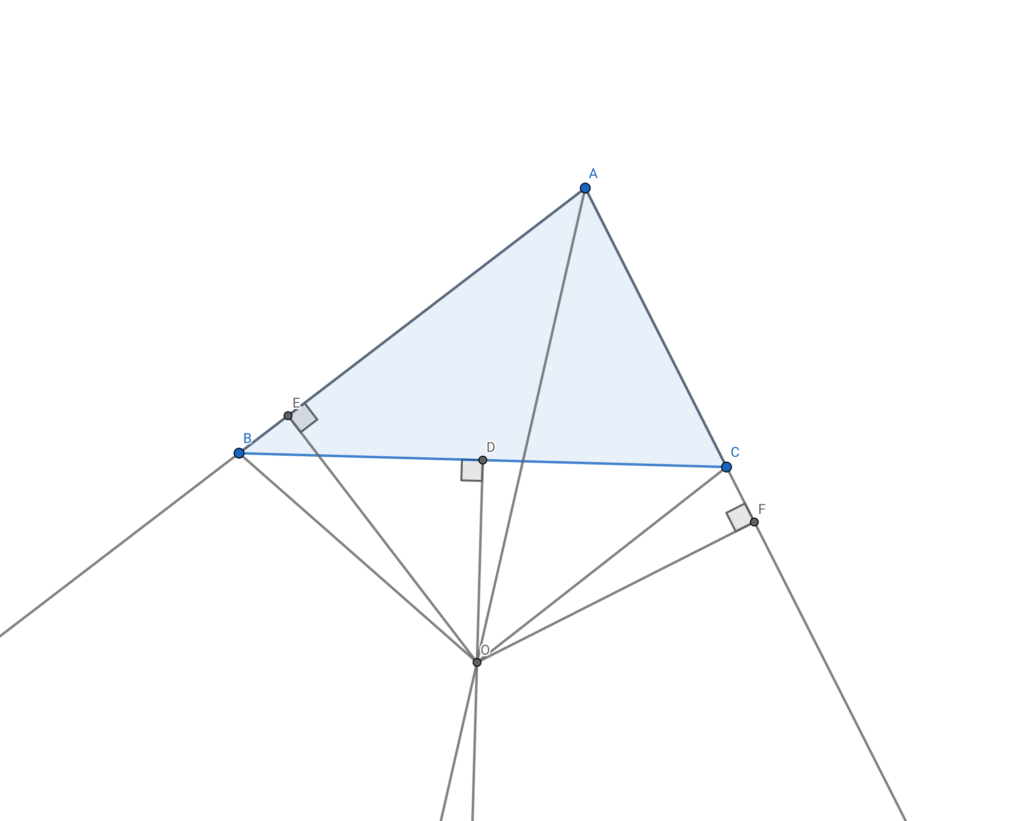
最初に提示した手書きの図と比べると、点Eの位置が違います。
この位置関係ならば、AE=AF、BE=BFは成り立っても、ABとACは等しいとは言えないのです。
では、なぜ手書きの図は起こり得ないと言えるんでしょうか?
これから証明してい来ますが、まず前提として、点Bと点E、点 Cと点Fはそれぞれ一致することはあり得ないことは前提とします。
なぜなら、もし点Bと点Eが一致したら、OB=OEで、OB=OC、OE=OFよりOC=OFとなり、点Cと点Fも一致し、この時AB=ACの二等辺三角形となるからである。
AB≠ACのとき下のような図が成り立つ、すなわち、AB<AEかつAC<AFが成り立つと仮定します。
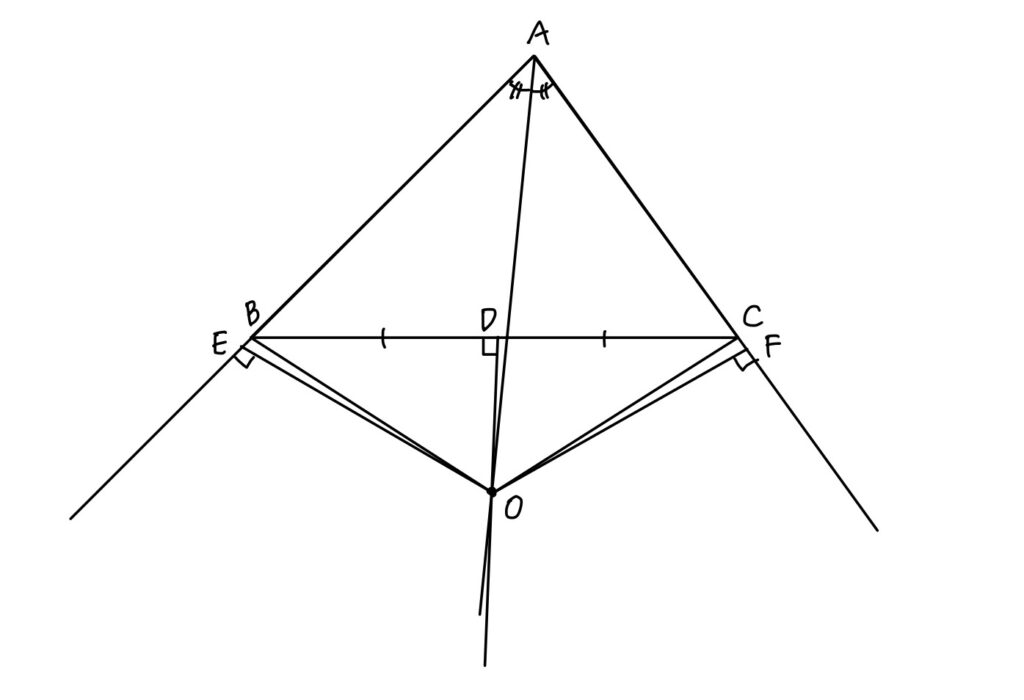
△AOEと△AOFは合同な図形より、AE=AF・・・⑦
△OBEと△OCFは合同な図形より、EB=FC・・・⑧
AB=AE-BE、AC=AF-FCと⑦、⑧より、AB=ACとなり、仮定に反します。
よって、「AB<AE」と「AC<AF」が同時に成り立つことは起こり得ないことになります。
言い換えると、「AB<AEかつAC>AF」か「AB>AEかつAC<AF」か「「AB>AEかつAC>AF」のいずれかが起こりうるということです。
しかし、AB>AEかつAC>AFのときも同様に矛盾することが言えます。(証明は同じような感じなので省略します)
よって「AB<AEかつAC>AF」か「AB>AEかつAC<AF」のいずれかが成り立たなければならないので、手書きの図は矛盾であると言えます。(証明終)
いや〜なんだかめんどくさい証明になってしまいましたね。
「図が変じゃん!」と言えば一発なのですが、じゃあ何が変なのかをちゃんと証明するには数学的な知識が必要な問題でしたね。
それでは!

コメント