こんにちは!さとあずです。
皆さん、暇つぶしなどで一度はこんなゲームしたことありませんか?
今、皆さんの前に格子柄があったとします。 左下のマスからスタートし、右斜め上にマスを通っていく。 すると、何マスか進むと壁にぶつかるので、反射するようにまた斜めにマスを通っていく。 また壁にぶつかったら、同じように反射して進む。 これを繰り返していくと、角に到達しそこから進めなくなり、ゲーム終了。
この勝ちも負けもないゲーム、一体このゲームのどこが面白いんだ?と思う人が多いとは思いますが、つまらない会議とか、勉強始めたけどやる気スイッチが出ない時とか、とりあえず暇つぶしに意味もなくマス目を斜めに埋めちゃうのって、あるあるじゃないですか?(笑)
しかも、マス目の数によって、すんなり角に到達してゲーム終了する時もあるし、何回も壁にぶつかって反射してやっと角に到達する時もある。
暇潰しの割には奥の深いゲームです。
そこでさとあずは考えました。
この意味もないゲームに規則性はないのか?と。
「そんなめんどくさいことはやめて、とりあえず暇つぶしにマス塗り潰そうぜ」という心の声がはっきりと聞こえてはいましたが、頑張って考えてみました。
問題文の後に、さとあずがどうやって考えて答えを導いたかを詳しく書いています。
答え合わせだけしたい!という人は【方針】は読み飛ばしてください。
【問題】格子柄ゲーム
今、縦にmマス、横にnマスからなる格子柄がある。
次のルールに従い、マスを埋めていく。
①左下の角を塗りつぶしそこから斜め右上に向かってマスを塗りつぶす。
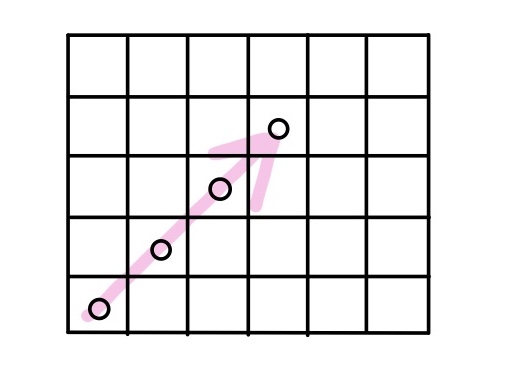
②端にたどり着いたら、壁に反射するように斜め右下または斜め左上に向かって進む。
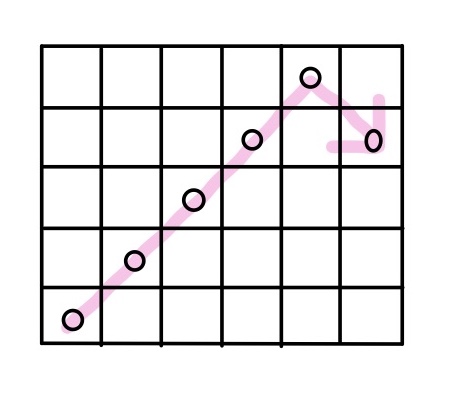
③また端にたどり着いたら、②と同様に反射するように進む。
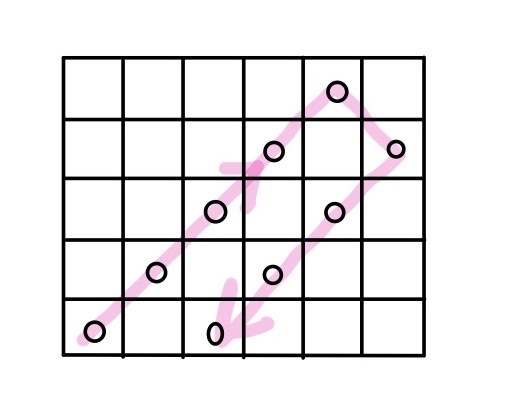
④これを角のマスにたどり着くまで繰り返す。
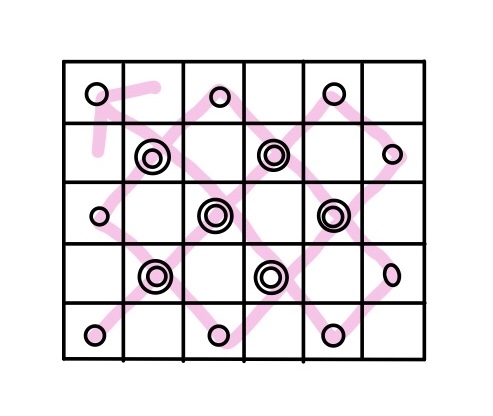
縦にmマス、横にnマスからなる格子柄は、左下の角をスタートし、他3つの角のいずれかに辿り着くまでに何マス通るだろうか。ただし、同じマスを通る場合は、通った回数分マスを数えるとする。
【方針】複雑な問題はとりあえず簡単になるまで分割して考えてみる
縦にmマス、横にnマスの組み合わせは無限にあるので全部検証するのは難しい。
だからと言って、思いつくままにランダムに確認するのは効率的とは言えないだろう。
そんな時は簡単な例から具体例で考えてみて、具体的なところで規則性を見つけ出すのが1つの方法である。
数学でも、「n番目の〇〇を求めよ」のような一般解を求める問題の時は、まずは具体的な例から考えて、なんとなく規則性が見えたら一般化を試みるのはよくある手法である。
【方針1】簡単な例から考えてみる
STEP 1 一度も折り返さない場合
まずは、一番シンプルな場合を考えてみましょう。
一度も折り返さないのは、m=nのときに起こりますね。
例えば、m=n=3のときは下図のようになる。
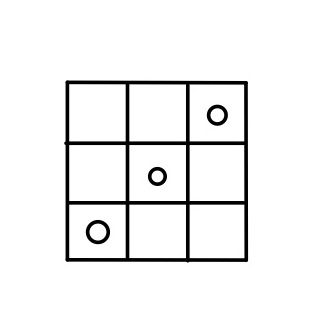
みた通り、3マス通る。
これの一般化は簡単ですね。縦横ともにmマスある場合は、m個のマスを通る。
STEP2 一度のみ折り返す場合
これは、例えば下図のようなm=3、n=5のとき
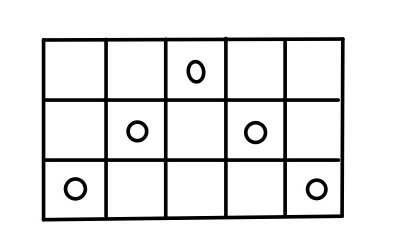
他にも、次のような例もある
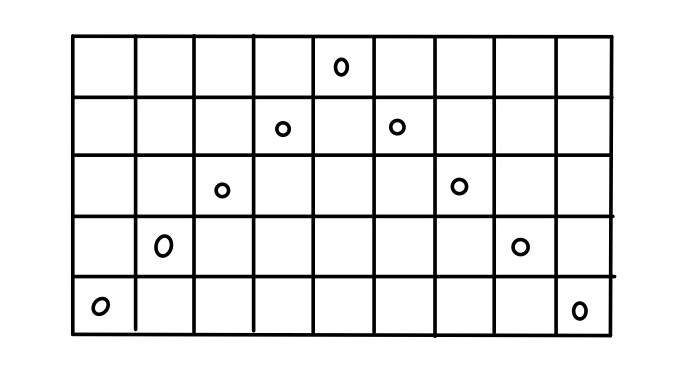
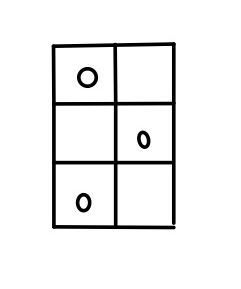
この例から、横のマスの方が縦のマスより多い時は、横のマス分のマスを通っていくので、n個のマスを通る。
STEP3 二度折り返す場合
これも考え方としてはSTEP2と同じですね
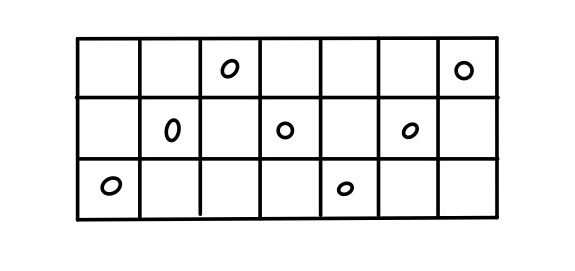
STEP4 三度折り返す場合
ここからは先ほどのように単純には行かない。
先程までのように、ひたすら右に向かって上下するものもあるが、左に引き返すものもある。
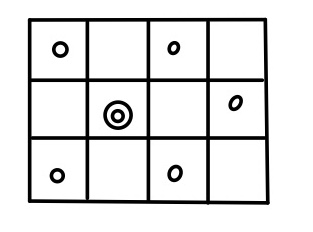
この形を今までと同じように考えるなら、下図のように後半のマスを移動させて考えてみるのはどうだろうか。
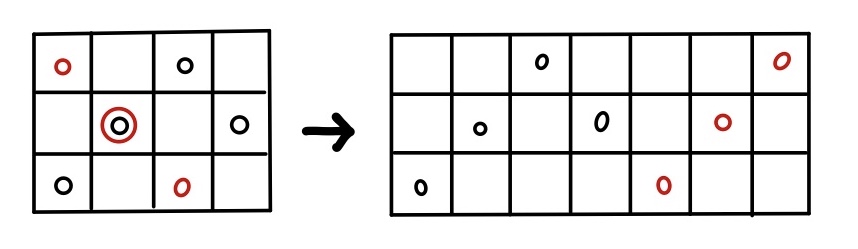
この例を見ると、右に進もうが左に進もうが、結局上下にジグザグに動いているのと変わらないことがわかる。
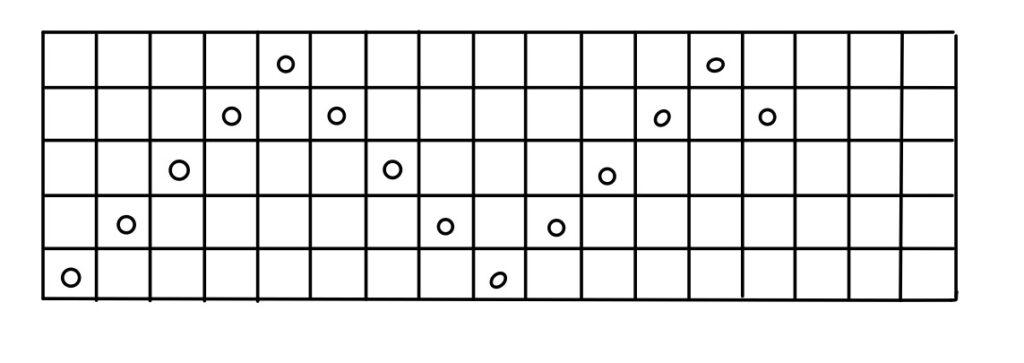
例えば、4回以上折り返すような下の例も書き換えれば結局上下にジグザグ動いているのと変わらない。
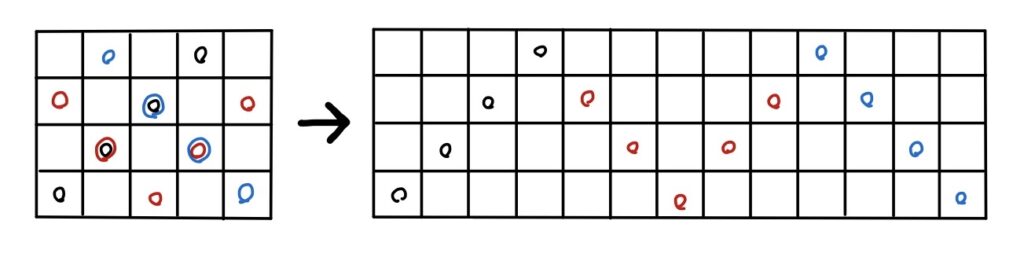
また、角で終わるということは、ジグザグも中途半端なところで終わることはない。
【方針2】何となく規則性が見えてきたら、今の段階の規則性を整理してマス目を数えてみる
【方針1】で具体例で考えたことで、どんな場合でもジグザグの形に書き換えることができることが分かった。
なので、ジグザグの形になった時のマス目の数え方を考えてみる。
最初から一般化したらこんがらがってしまうので、まずは次のような縦5マスの場合で考えてみよう。
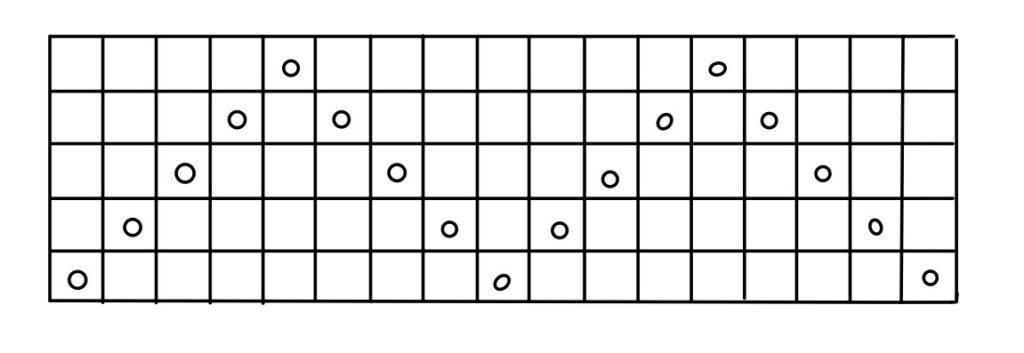
この場合、答えは数え上げれば17マスだが、これを計算で出してみよう。
計算式で出してみる方法は何通りか考えられる。
例えば、縦のマスの数に上下した回数をかけて、ダブりを引く方法がある。
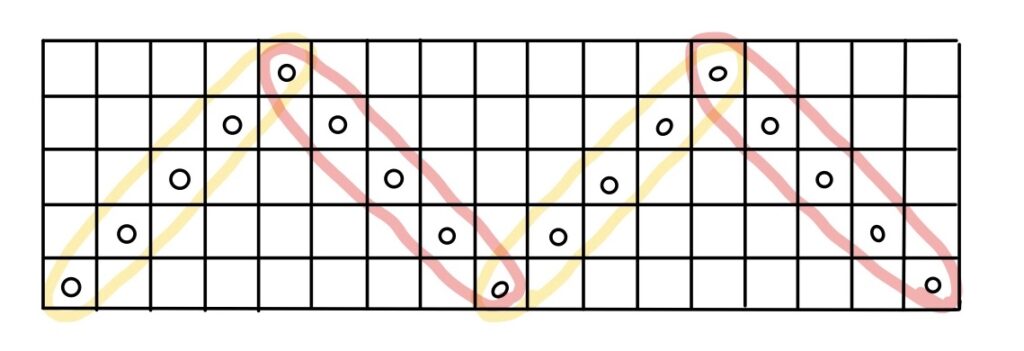
この場合、縦5マスを4回上下していて、3箇所のダブりがあるので5×4−3=17
この場合だと、縦mマスをk回上下した場合、mkー(k-1)=mk-k+1個のマスを通ると言える
ダブりを引く方法以外には次のような考え方もできる。
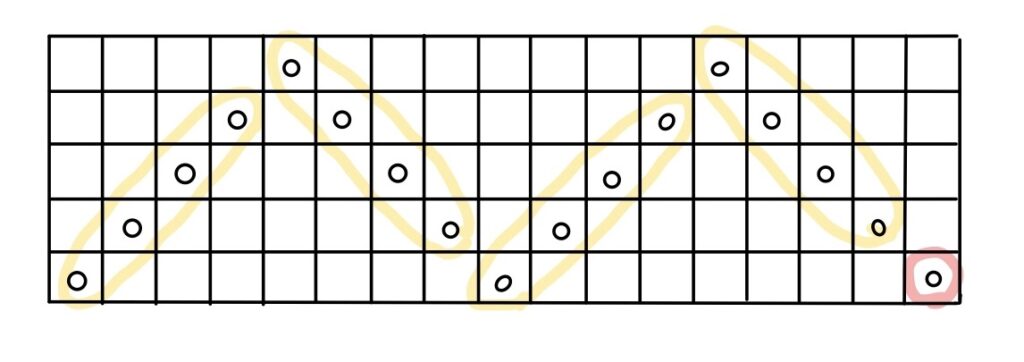
この場合だと、4×4+1=17
この考え方の場合、(m-1)k+1=mk-k+1
いずれにせよ、何回上下するかがわかれば通るマスの数も数えることが可能であると分かった。
【方針3】何往復するか検討する
どのパターンもジグザグに上下する進み方に書き換えられることが分かったから、あとは”何回ジグザグするか”が分かれば良い!
先ほどは上下にジグザグする場合にかきかえたが、見方を変えれば左右にジグザグするとも見れる。
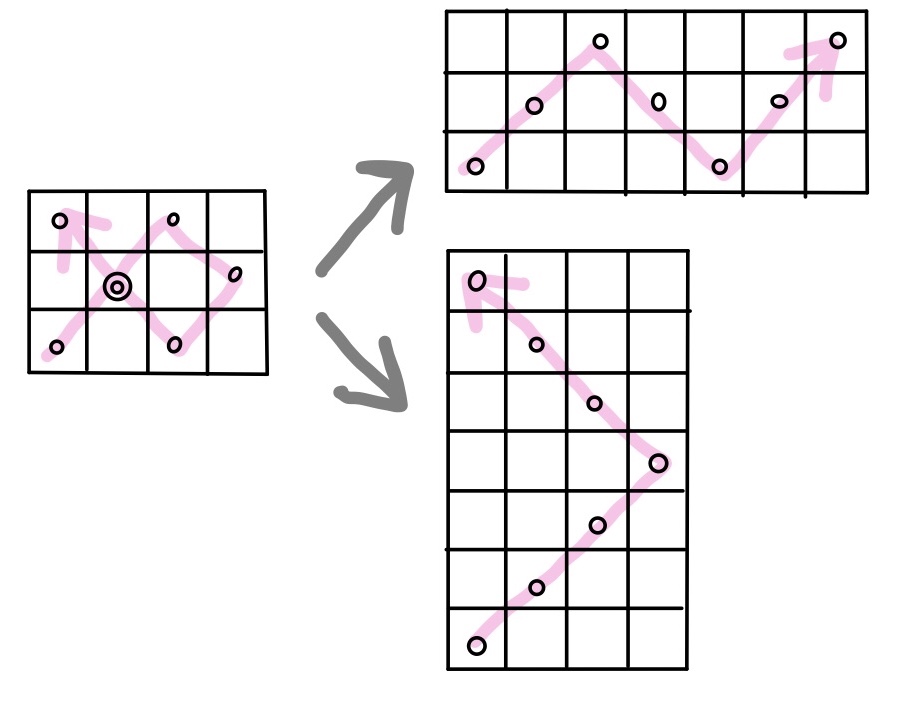
今、縦mマス横nマスについてマスを進めたものを、上の図のように上下のジグザグと左右のジグザグに書き換えたとする。
仮に上下にはk回、折り返しがあったとすると、通るマスの個数は(m-1)k+1
左右にs回の折り返しがあったとすると、通るマスの個数はと(n-1)s+1
(m-1)k+1は「(m-1)の倍数+1」、(n-1)s+1は「「(n-1)の倍数+1」の形で、これらが一致するので
「(m-1)と(n-1)の最小公倍数+1」の形になることが推定される。
【解答】答えは1つの式で導ける!?
縦mマス、横nマスの左角からスタートし他の角に辿り着くまでに通るマスの個数は「(m-1)と(n-1)の最小公倍数+1」の形で表すことができます!
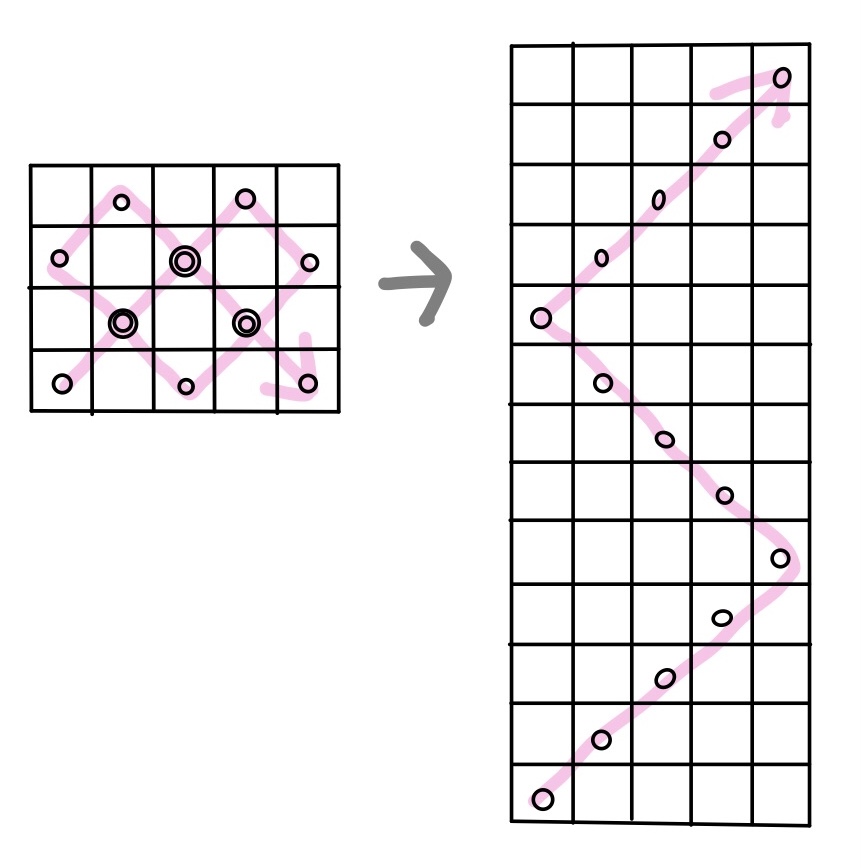
m=4、n=5の場合でもう一度考えてみよう。
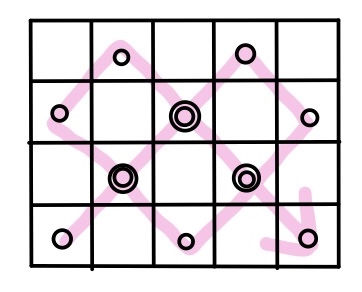
これを上下のジグザグに書き換えると下の図のようになる。
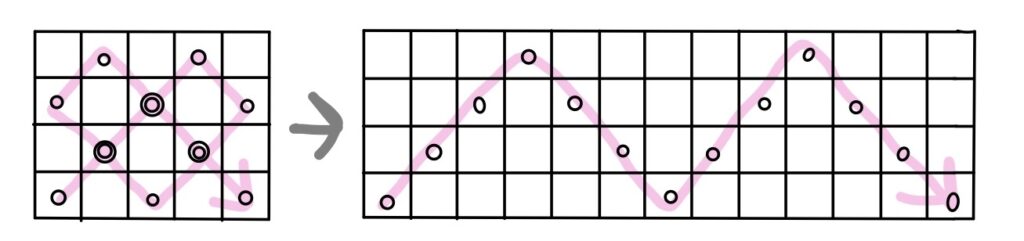
このゲームのルール上、角にたどり着いたときにゲーム終了なので、この上下のジグザグが上辺か下辺に辿り着かない状態で終了することはありえない。
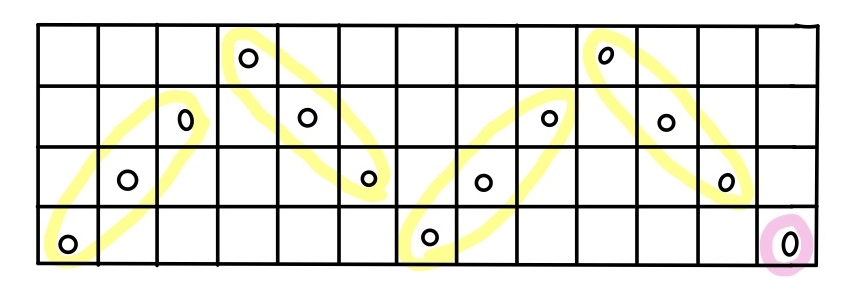
なので、通るマスの数は上のように考えられるので、「3の倍数+1」(m-1の倍数+1)の形でマスの個数は表せることがわかる。
同様に次は左右のジグザグに書き換えた場合も考える。
同様に角にたどり着いたときにゲーム終了なので、左右のジグザグが右辺か左辺に辿り着かない状態で終了することはありえない。
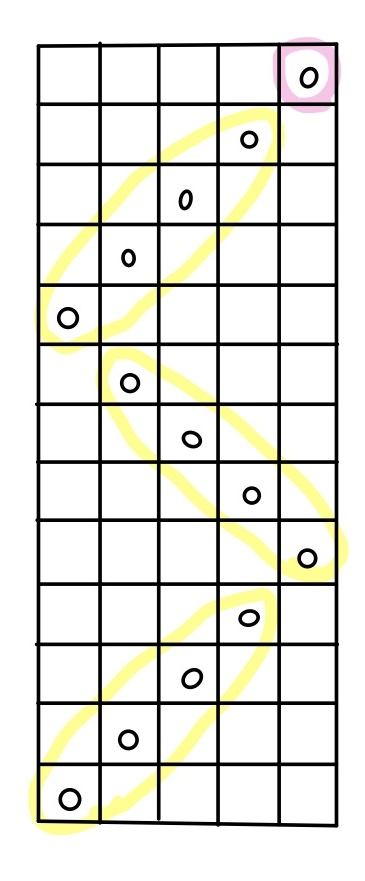
なので、通るマスの数は上のように考えられるので「4の倍数+1」(n-1の倍数+1)の形でマスの個数は表せることがわかる。
以上のことから、通るマスの個数は「3の倍数+1」(m-1の倍数+1)の形かつ「4の倍数+1」(n-1の倍数+1)の形で表せれば角にたどり着くことになるので、「3と4の最小公倍数+1」すなわち12+1=13個のマスを通る。
これを一般化すれば、縦mマス、横nマスの左角からスタートし他の角に辿り着くまでに通るマスの個数は「(m-1)と(n-1)の最小公倍数+1」の形で表すことができるといえます!

コメント