こんにちは!さとあずです。
今日は子どものおもちゃやアプリのゲームでもよくある「ハノイの塔」パズルを数学を使って紐解いていこうと思います!

ハノイの塔パズルのルール
3つの柱のうちの左側の柱に、複数の円盤が下にあるものが大きくなるように差し込まれている。次のルールに従い、全ての円盤を右側の柱にできる限り小さい手数で移す。
ルール① 円盤は1つずつ動かし、3つの柱のどこかにさしこむ。
ルール② 下にある円盤より大きい円盤を上に置くことはできない。
例えば2つの円盤の場合、下の図のように3回の操作で移すことができますね。
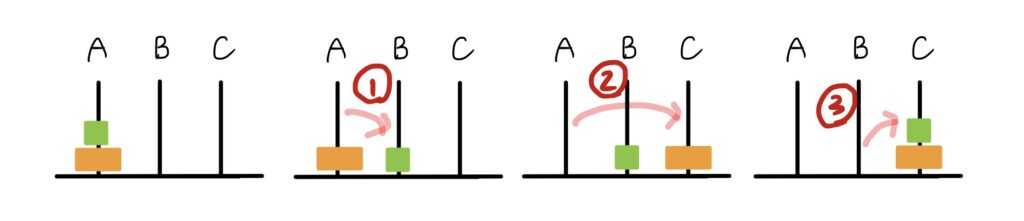
ハノイの塔パズルを使った数学の問題
ハノイの塔の問題を数学風に表すとこんな問題になります。
n枚の円盤を移す最小の操作の回数がan回だとする。 (1)3つの円盤を移す時の最小の操作の回数a3を求めよ。 (2)an+1をanを使って表せ。 (3)anを求めよ。
〜〜〜〜(1)の解説〜〜〜〜

(1)は3枚の円盤を移せばいいんだよね!
3つの大きさが違う積み木があればなんとか出せそう!!

あずきちゃん、その調子だ!
消しゴムでも空箱でもなんでもいいから実験してみよう!!
どんな難しい問題も、「小さい数から具体的に」考えてみるのが第一歩だよ。

んん〜〜パズルみたいで難しいぞ〜

すごく頑張ってる!
まず第一手は、一番小さい円盤を一番右の柱に置くことから始めてみるといいよ

なるほど!これで7回!どうだ!

正解!さすが!
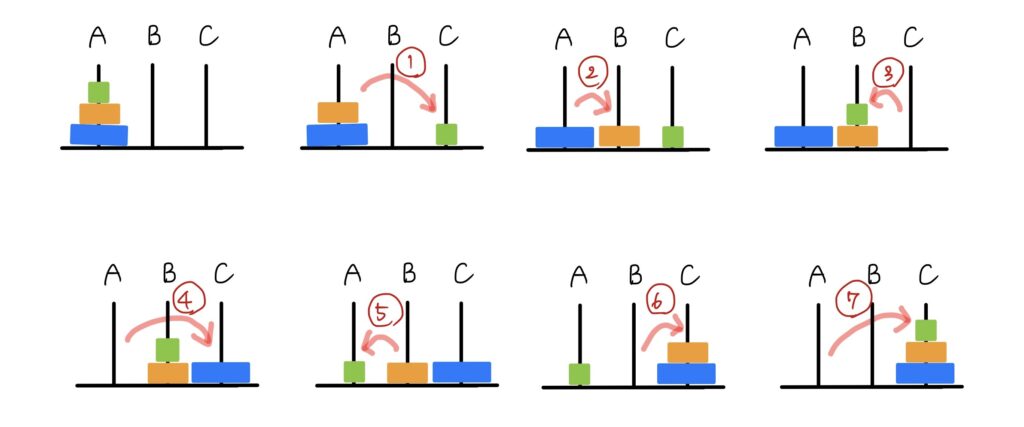
a3=7(回)が正解となります。
〜〜〜〜(2)の解説〜〜〜〜

an+1をanを使って表す?
nが出てきたら急にわからなくなった〜〜〜(泣)
もうやめる〜〜〜

まあまあ、冷静にいきましょうよ。
わからなくなったらまずは具体的に考えてみるのが一番の近道!
n=2として考えてみたらどうかな?

n=2として考えたら「a3をa2を使って表す」かあ。
a2=3, a3=7だよね。a3=a2+4だな!!

まあ、a2とa3だけだったら間違いではないね(笑)
「3枚の円盤を移す」過程の中に「2枚の円盤を移す」ときの過程が見つけられないかな?
2つの過程をもう一度見比べてみよう
〔2枚の場合〕
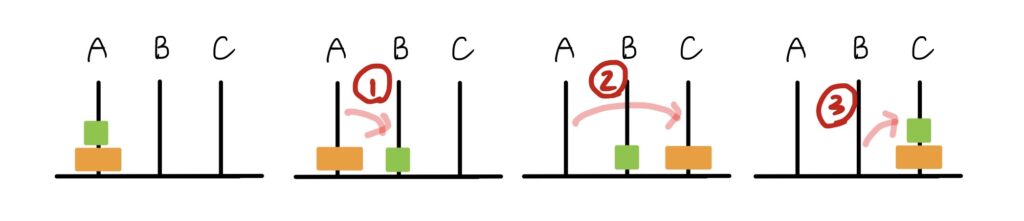
〔3枚の場合〕
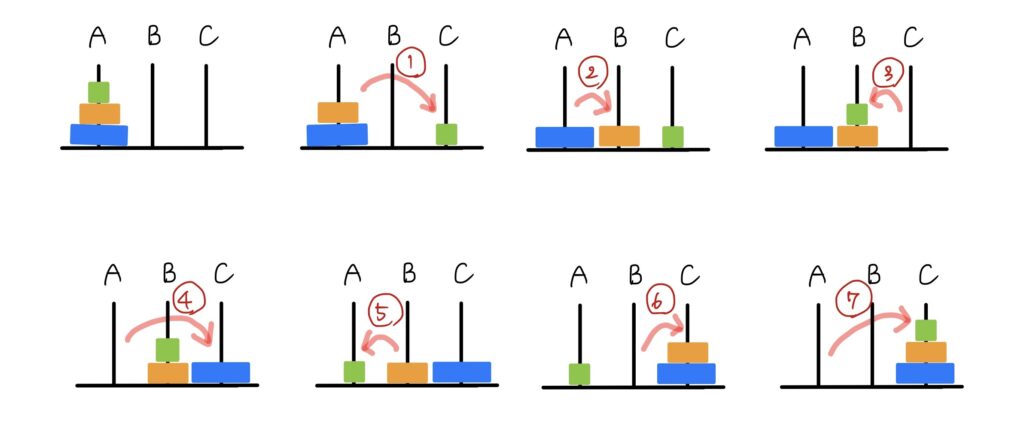

3枚の時の①②③って、2枚の時の①②③と似てるね。
3枚のうちの上の2つを他の柱に移しているんだね

おお!いいところに気づいたね。
2枚を他の柱に動かしているところが他にもないかな?

あ!⑤⑥⑦も2枚を他の柱に移しているね!
3枚動かすときに、2枚動かす方法を2回使っているんだね

いいことに気づいたね!
あずきちゃんの考えを図でまとめるとこんな感じかな!
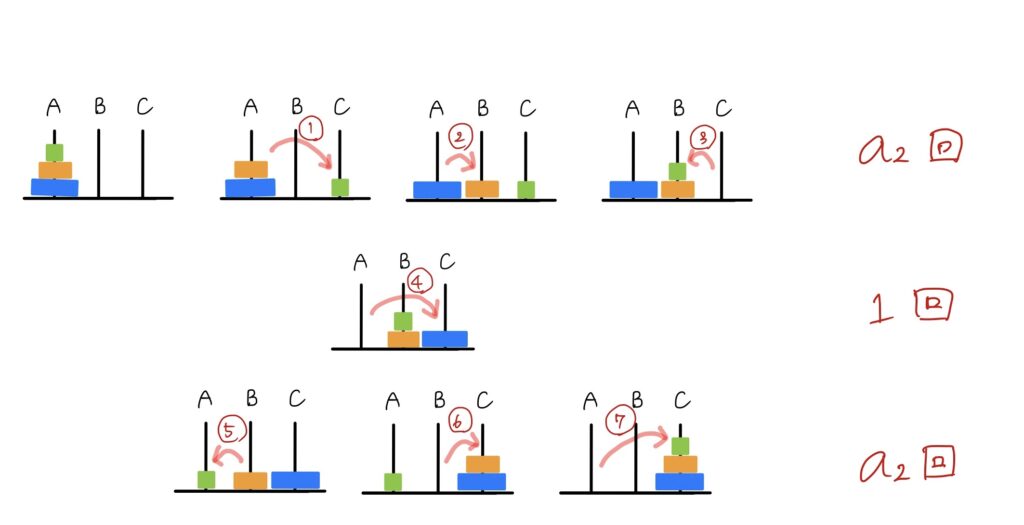
このことからa3=a2+1+a2=2a2+1すなわち、a3=2a2+1と表せる事になります。

こう考えると、a3とa4の関係もa4とa5の関係も同じように考えられそうだね

そうだね!
4枚の円盤を移す場合(a4回)は、上の3枚の円盤を真ん中の柱に移すのにa3回、一番大きい円盤を右の柱に移すのに1回、真ん中の3枚の円盤を右の柱に移すのにa3回の操作が必要だから、a4=2a3+1と表せるね。
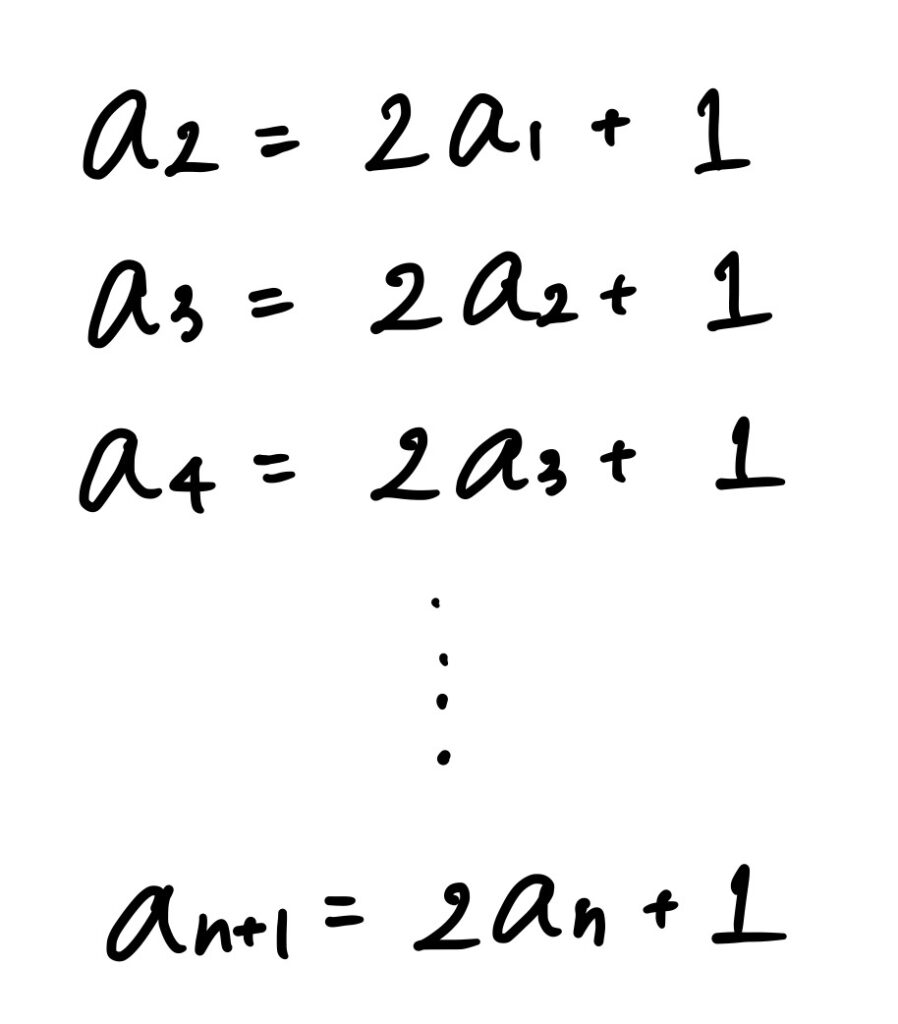

じゃあ、(2)の答えはan+1=2an+1だ!

正解!
ちなみに、an+1=2an+1のような式を数列{an}の漸化式というよ。
この場合、初項a1がわかれば、a2やa3といった他の項もどんどん求められるね。
a1がわからないと他の項が出ないから、an+1=2an+1のような2項間漸化式の場合は初項と一緒に表すのが大原則だよ。
a1=1、 an+1=2an+1
〜〜〜〜(3)の解説〜〜〜〜

漸化式から一般項anを求める方法を教えるよ。
まず、an+1=2an+1のan+1とanをα(アルファ)と置き直して、その方程式(注1)を解く。
α=2α+1 より α=−1
次のような計算をすると、an+1=2an+1はan+1+1=2(an+1)と変形できる。

数列{an+1}は初項がa1+1=2、公比が2の等比数列(注2)なので、
an+1=2×2n-1=2n
よって、an=2n−1
(注1)特性方程式という
(注2)等比数列とは、初項にある同じ数をかけると次の項になるような数列です。
例えば、数列{2,6,18,54,162,・・・}は初項が2で、初項に3をかけると第2項、第2項に3をかけると18・・・となります。この時の「3」を「公比」といいます。

なんか(3)だけ色々説明飛ばしてない?

ぐぬぬ。あずきちゃん鋭い・・・
等比数列の公式とかは完全にすっ飛ばしました。ごめんなさい!
また、ご要望があれば説明します〜〜〜
Colum ハノイの塔の伝説
ハノイの塔は、フランスの数学者エドゥアール・リュカが1883年に発売したゲームがルーツであると言われています。
そのゲームのリーフレットにはこんなお話が書かれているそうです。
今から約5000年前のこと。インドのガンジス川の畔に世界の中心を表す巨大な寺院がありました。天地創造の神はそこに、3つのダイヤの柱と、中心に穴の空いた64枚の純金の円盤が、円盤が下から大きい順に1つの柱に刺さるように置きました。そして、そこの僧侶たちにこう述べたのです。 「この64枚の円盤を一度に一枚ずつ別の柱に移しなさい。全ての円盤が移し終わった時に、世界は崩壊し終焉を迎えます」(ルールは前述の通り)
まだこの世界は崩壊していないので、きっと今頃も僧侶たちは円盤を1つずつ移しているかもしれませんね。
さて、64枚の円盤を移し終えるには、どのくらいの時間がかかると思いますか?
仮に1枚移すのに1秒かかるとして、264-1秒かかります。
これ、年数に換算すると約5845億年です。
しばらくこの世界に安心して生きていられそうですね。
ちなみに、子ども用のおもちゃのハノイの塔は10枚なので、10枚の場合も計算してみましょう。
210-1=1023
1枚1秒だとすると、1023秒=17分3秒かかります!
実際、1枚を1秒で動かせる人がいたら神業なので、もう少しかかりそうですが1時間あればおわりますかね??
まとめ
今回のお題は子ども用のおもちゃを使っている割には、内容はバリバリ高校数学で難しかったかもしれませんね。
さとあずがこの問題で伝えたかったことは、
「難しい!わからない!と思う問題は、わかるところまで小さく具体的にしてから考える」
ということです。
数学って、文字が出てきた途端に嫌になってしまうことってありますよね。
数学で出てくるxとかnとかって、そこにいろんな数を入れることができるから便利なんですが、いろんな数を入れられるから複雑でわかりにくくなってしまうんですよね。
だから、そんな時は具体的な数字を入れてできるだけ簡単に考えてみるだけで、「あ、なんだこんなことが言いたかっただけなのか」「これだったらできるかも!」と思えるかもしれません。
数学に限らず、仕事とか家事とかだって、そうですよね。
育児中のさとあずはいつも、

「わ〜〜も〜〜なんか家は散らかってるし、ちびあずは泣いちゃってるし、やることがたくさんでもう何から手をつけていいかわからない〜〜〜」
と、いつも言っていますが、これもやることをもっと小さく分けて、できることからやっていけば、気づいた時には全部片付いてたりするわけです。(結局片付かないことも多いけれども(笑))
少しでも参考になれば嬉しいです。
そんじゃ!



コメント