こんにちは!さとあずです。
さとあずは、前々からずっと欲しいおもちゃがありまして。。。
それが、ポリドロン!!!

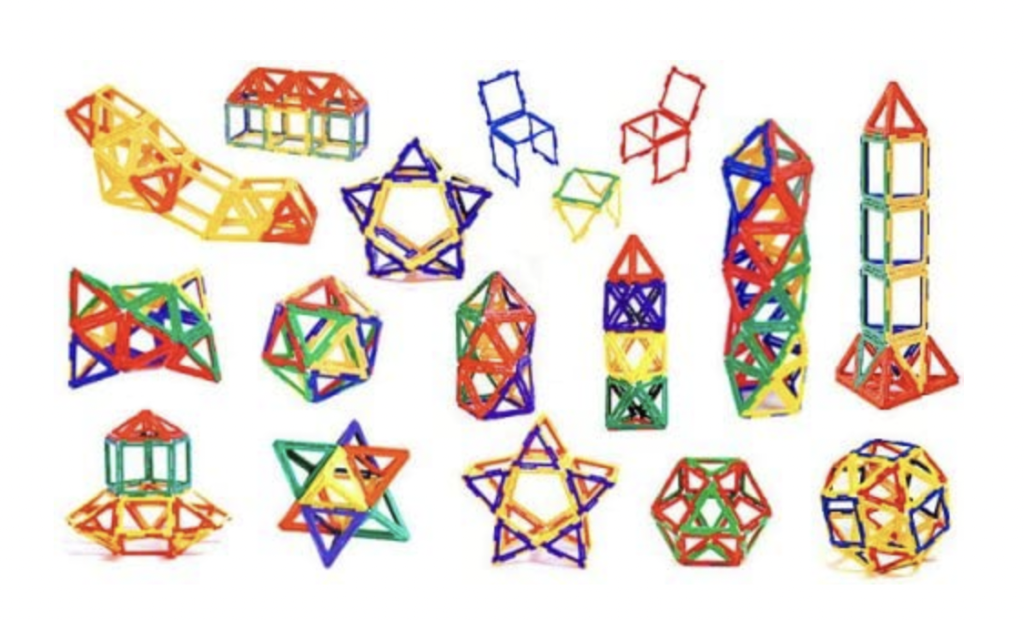
ポリドロンは正三角形や正方形などのパーツを組み合わせていろんな立体が作れるおもちゃで、東京書籍という教科書会社から発売されているのもあり、知育おもちゃとしても期待できたりします。
これでいろんな多面体を作りたい!!!
でも必要不可欠なわけではないんだよな〜
ドケチなさとあずは、欲しくてもなかなか購入できずにいるのですが、
きっとちびあずちゃん(0歳)がこれで遊べる年齢になったら、
「おもちゃ欲しいよね?ね?欲しいよね?」
とかなんとか理由こじつけて買う予定です(笑)
前置きが長くなりましたが、今回はポリドロンでも作ることができる「切頂二十面体」についてお話していきます!
なんだか聞きなれない名前ですが、サッカーボールも「切頂二十面体」なんですよ。
「切頂二十面体」の奥深いお話ぜひ最後まで読んでみてください〜
「切頂二十面体」って何?
切頂二十面体はその名の通り「正二十面体の頂点を切ったもの」です。

え、頂点を切る?どういうこと?
そもそも正二十面体って何?
という方のために、
①正二十面体って何? ②頂点を切るってどういうこと? ③切頂二十面体ってどんな立体?
という3つに分けて噛み砕いて説明します。
①正二十面体って何?
そもそも正〇〇面体と呼ばれる立体は、「正多面体」と呼ばれています。
正多面体の定義は「全ての面が同じ正多角形(正三角形or正方形or正五角形)でできており、かつすべての頂点において接する面の数が等しい凸多面体」です。
正多面体は「正四面体、正六面体、正八面体、正十二面体、正二十面体」の5つしかありません。
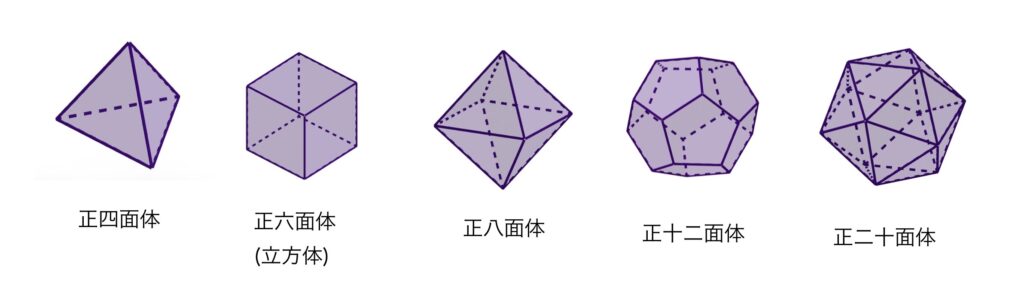
正多面体の中でも一番面の数が多い、正二十面体は20枚の正三角形の面からできています。
1つの頂点に5つの正三角形が接しているのが特徴です。
ちなみに、正二十面体の頂点の数は12個、辺の数は30個です。(のちに詳しく解説しますね)
②頂点を切るってどういうこと?
頂点を切ると言っても、適当に切っていいわけではなく、正確には、
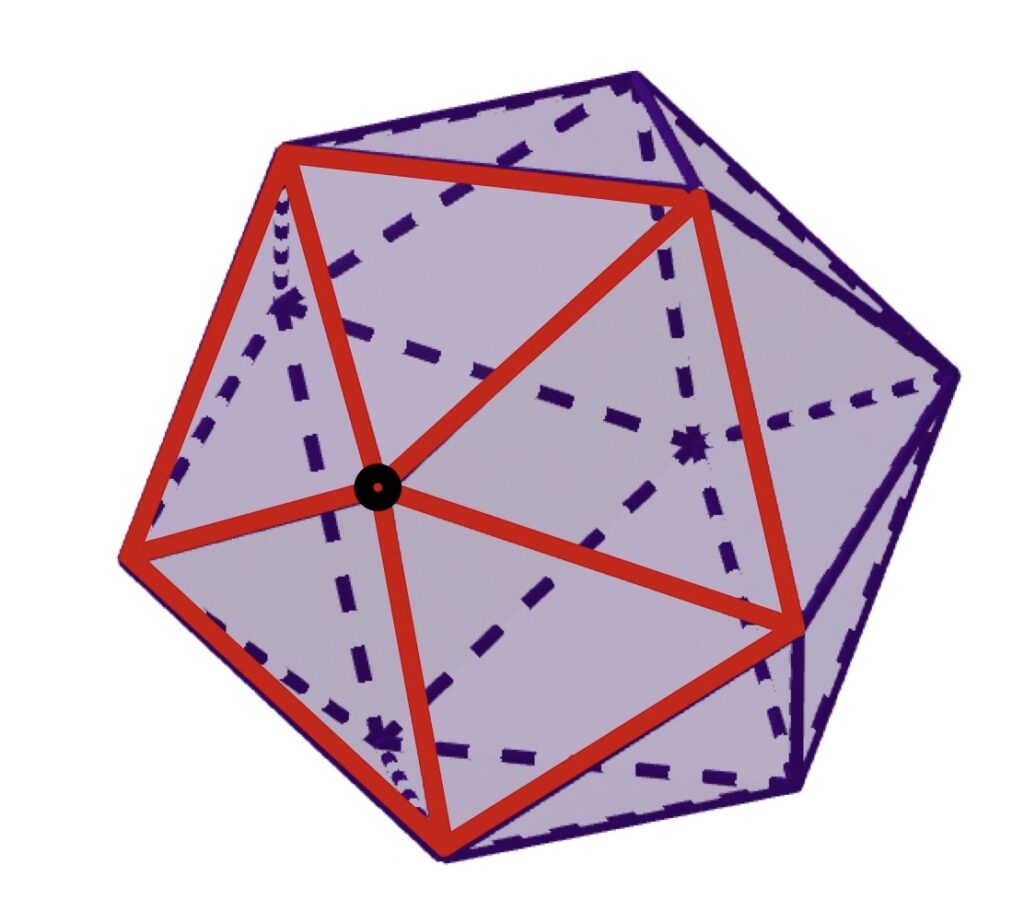
「正二十面体の各頂点を、各辺を3等分する点を通る平面で切り落とす」
ということです。
正二十面体は、1つの頂点に5つの正三角形が接しています。
言い換えると、1つの頂点に5つの辺が集まっていることになりますね。
その各辺を3等分する点を通る平面で切り落とすと、5つの辺から1つずつ頂点が作られるので断面は正五角形になります。
③ 切頂二十面体ってどんな立体?
正二十面体は20個の正三角形でできた立体ですが、切頂二十面体の面はどんな形になっているでしょうか。
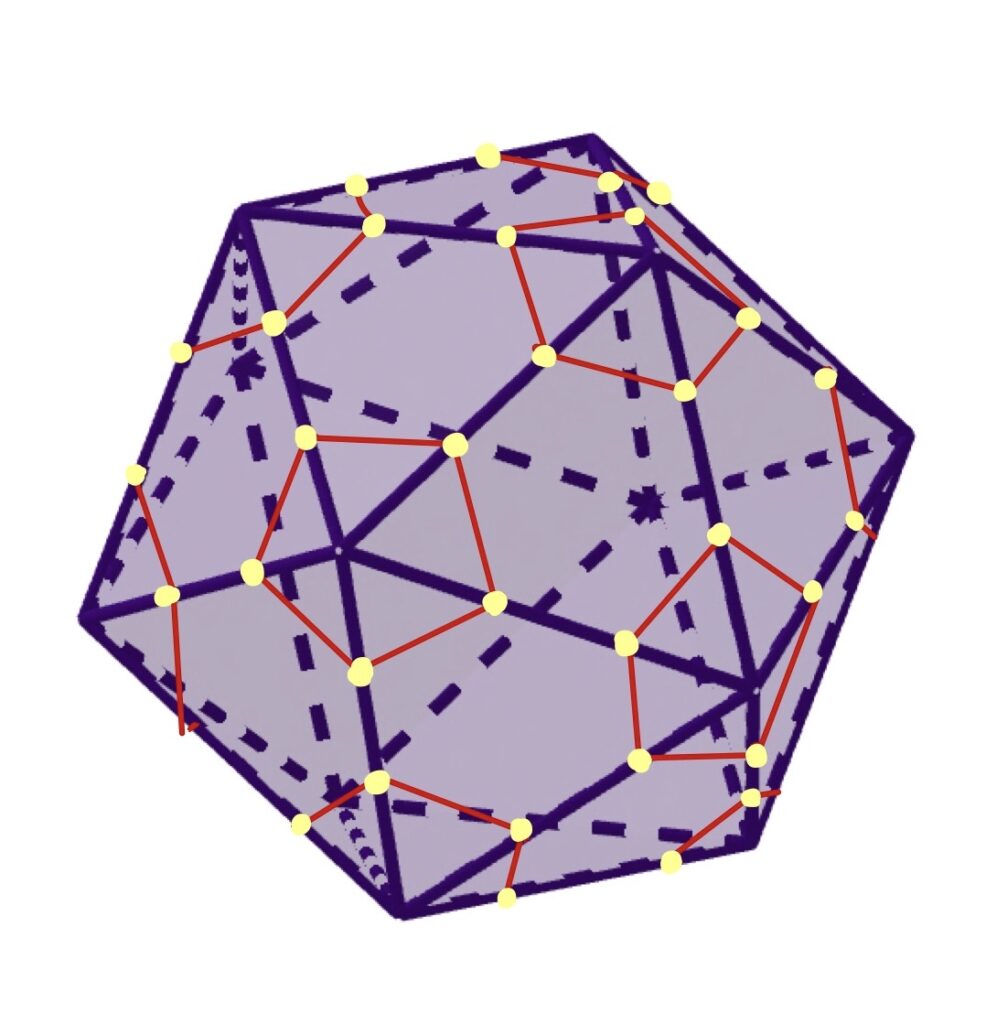
まず、正三角形だった面は、各辺の3等分する点で切り取られるので、正六角形になります。
正二十面体の正三角形20個が切り取られることによって正六角形になるので、切頂二十面体の正六角形の個数も20個ですね。
また、頂点を切るとき、正二十面体の各頂点は5つの面が接していたので、断面は正五角形になりました。
正二十面体の頂点の数は12個なので、切頂二十面体の正五角形の数も12個ということになります。
実際にサッカーボールの画像をみてみましょう。

サッカーボールの白い部分は正六角形、黒い部分は正五角形になってますね。
切頂二十面体の辺、面、頂点の数を数えてみよう〜!!

さて、「切頂二十面体」がどんな立体かなんとなくわかったところで、切頂二十面体の辺、面、頂点の数を数えていきましょう〜!!
急に切頂二十面体を扱うのは難しいので、正多面体の辺、面、頂点の数えてみましょう〜
(例) 正八面体の辺、面、頂点の数
例えば、正八面体は、辺の数が12、面の数が8、点の数が6ですね。
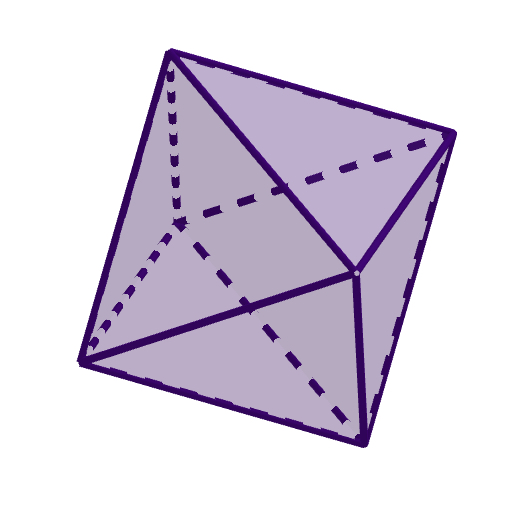
これをあえて計算で求めてみます。
正八面体は「正三角形の面が8つ」からできている正多面体なので、面の数は8。
三角形が8つあるので、ダブりを無視すると3×8=24の辺があるのですが、それだと立体にしたときに1つの辺を2回ずつ数えてしまっているので3×8÷2=12個となります。
頂点も同様に、三角形が8つあるので、ダブりを無視すると3×8=24の頂点があるのですが、立体にしたときに1つの頂点を4回数えているので3×8÷4=6個となります。
正多面体の面、辺、頂点の求め方はこんな感じです。
それでは、正二十面体も同じように求めてみましょう〜!
正二十面体の辺、面、頂点の数
正二十面体は「正三角形の面が20個」からできている正多面体なので、面の数は20。
辺が3つの正三角形が20個あり、3×20だと辺を2回ずつダブって数えているので、3×20÷2=30個
頂点が3つの正三角形が20個あり、3×20だと頂点を5回ずつダブって数えているので、3×20÷5=12個
よって、正二十面体の面の数は20、辺の数は30、頂点の数は12ということになります。
切頂二十面体の辺、面、頂点の数
まず、切頂二十面体の面は正六角形の面と正五角形の面があります。
正六角形の面は、正二十面体の正三角形の面からできたものなので、正二十面体の面の数と同じ20個。
正五角形の面は、正二十面体の頂点を切ってできた断面なので、正二十面体の頂点の数と同じ12個。
つまり、切頂二十面体の面の数は正六角形が20個、正五角形が12個、合計32個です。
次に辺です。正六角形が20個、正五角形が12個なので、ダブりを無視して辺の数を数えると6×20+5×12=180。これだと、立体にしたときに1つの辺を2回ずつ数えているので180÷2=90個になります。
最後に頂点も同様に考えます。正六角形が20個、正五角形が12個なので、ダブりを無視して頂点の数を数えると6×20+5×12=180。1つの頂点を3回ずつ数えているので180÷3=60個
つまり、切頂二十面体の面は32個、辺は90個、頂点は60個ということになります。

あ〜難しかった〜!お腹いっぱい〜!
でも、立体の面、辺、頂点の数を計算で求められるなんて知らなかったよ〜

1個1個数えるとどうしてもミスが出てしまうから、こうやって計算で求められるといいよね。
ちなみに、全ての多面体の面、辺、頂点の数にはある共通の性質があるんだよ。
凸多面体における頂点の数をv、辺の数をe、面の数をfとしたとき、v-e+f=2が常に成り立つ。

これは「オイラーの多面体定理」という有名な定理なんだよ。
詳しい証明は別記事にするけど、今回やった正多面体や切頂二十面体もこの定理に当てはまるのがわかるよ。
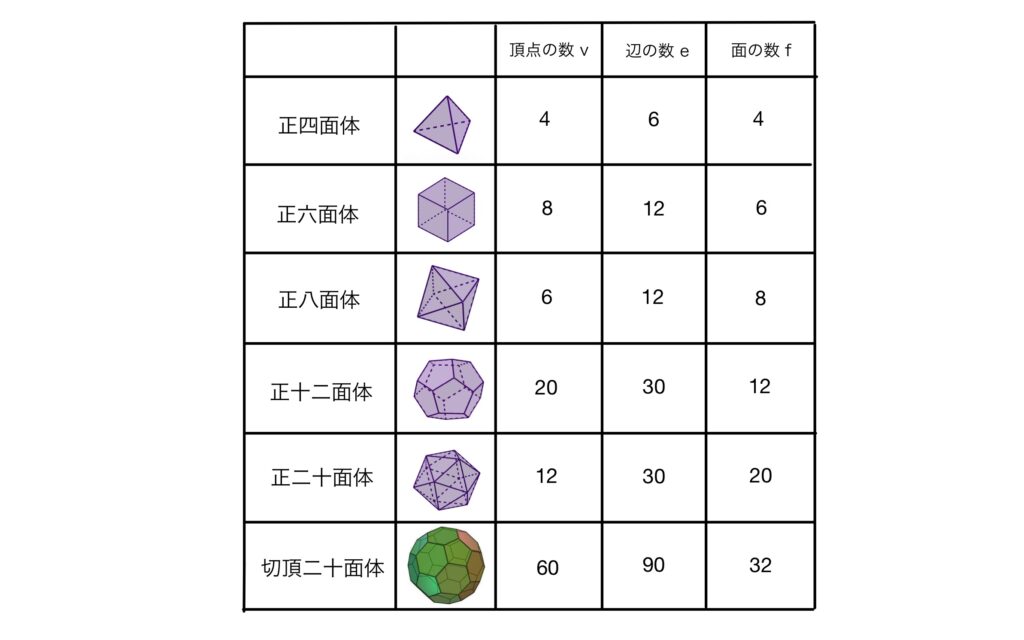

ほんとだ〜!不思議だね!
切頂二十面体仲間のフラーレンの不思議なお話

「切頂二十面体」の形をしているものはサッカーボール以外にも、炭素の同素体である「フラーレン」の一種の炭素原子が60個結合してできた物質も同じ形をしているんだよ。
ここでは、フラーレンについて数学的に深掘りしていくよ〜
さとあずは化学は全く専門じゃないので、あくまでも数学的に考えたらこんな面白いことがあったよ〜というお話です。
サッカーボールと同じ形をしているフラーレンは、切頂二十面体の頂点の部分に炭素原子が配置されている形になっているので、切頂二十面体の頂点の数と同じ60個の炭素原子からできています。

C60と表します。
フラーレンは他にも炭素原子の数が70個、76個、80個のものなどが見つかっていて、どれもC60と同じように全ての面が正五角形や正六角形で構成された形になっています。
しかし、炭素原子の数をどれだけ増やしても正五角形の数は一定なんです!!

つまり、炭素原子の数を変えたら、正六角形の数だけが変わるということ??
切頂二十面体の正五角形の数は12個だったから、炭素の数が変わっても正五角形は12個のままってことかな?

そうそう!あくまで正五角形と正六角形だけの面で成り立っている前提だけど、炭素の数が変わっても正五角形の数が変わらないのは不思議だよね〜
証明はオイラーの多面体定理を使うよ!
証明
フラーレンの頂点の数、辺の数、面の数をそれぞれv,e,fとする。
また、フラーレンの形を構成する正五角形の数をxとする。
この時、正六角形の数はf-x
正五角形の1つの内角は108°、正六角形の1つの内角は120°より、多面体の1つの頂点に集まる面の組み合わせは「正五角形3つ」「正五角形2つ+正六角形1つ」「正五角形1つ+正六角形2つ」の3通りしかない(注1)ので、多面体のどの頂点も1つの頂点に3つの面が接していることになる。
よって、次の式が成り立つ
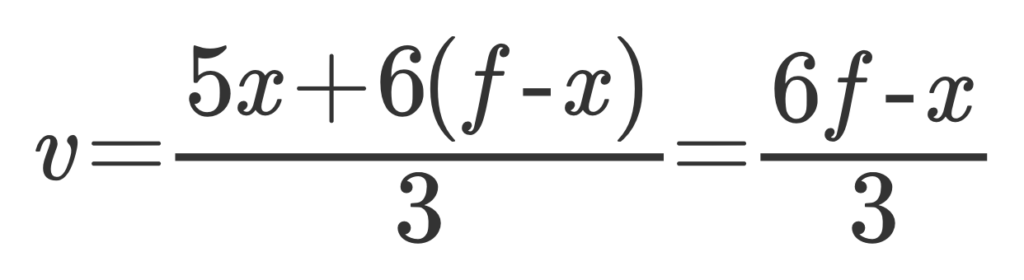
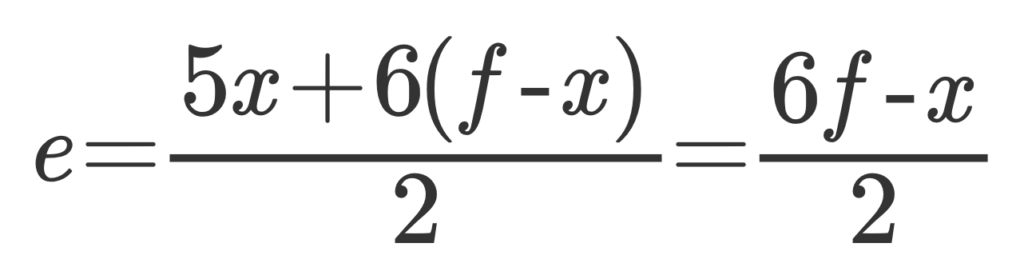
オイラーの多面体定理より、v-e+f=2が成り立つので
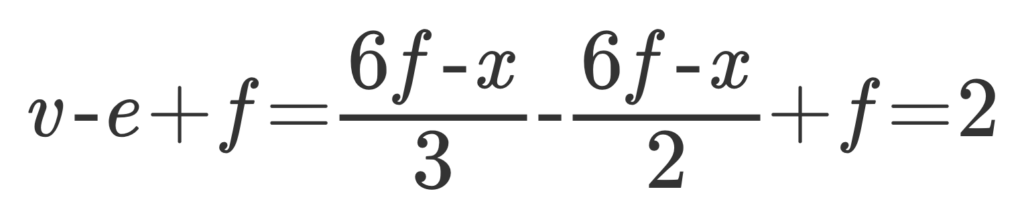
これを計算するとx=12
よって、正五角形の数はv,e,fの値によらず常に12で一定である。(証明終)
(注1)多面体の1つの頂点に集まる角は3つ以上で、それらの和は360°未満でないといけません。360°だと平面になってしまうから頂点ができないし、360°以上だと立体にすることができないからです。また1つや2つの角だと立体にできませんよね。
少しでも参考になったら嬉しいです。
それでは!



コメント